Appunti sulle Antenne
Table of Contents
Oggi parliamo delle antenne, qui di seguito sono riportati dei miei personali appunti, buona lettura.
Propagazione delle onde elettromagnetiche nello spazio libero⌗
I parametri con cui si valuta l’entitá del campo elettromagnetico sono:
- Densitá di potenza \(S\) , che si misura in \(w / m^2\)
- Intensitá del campo elettrico \(E\), che si misura in \(V / m\)
In particolare, si deve garantire che sull’antenna ricevente si abbia un valore di campo elettromagnetico tale da ottenere in ingresso al ricevitore un segnale che abbia un livello di potenza pari alla sensibilitá del ricevitore.
La sensibilitá del ricevitore (in inglese sensitivity) é definita come il minimo livello di potenza del segnale in ingresso al ricevitore che consente di fornire in uscita un segnale di qualitá accettabile.
I valori del campo elettromagnetico dipendono da fattori come:
- Potenza del segnale fornito in ingresso all’antenna trasmittente
- Tipo di antenna trasmittente
- Distanza fra antenna trasmittente e ricevente
- Ambiente in cui avviene la propagazione delle onde elettromagnetiche
Altri due concetti importanti per lo studio dell’entitá del campo elettromagnetico sono: l’antenna isotropica e lo spazio libero.
Un’antenna isotropica ideale é un antenna che irradia uniformemente in tutte le direzioni dello spazio e non causa dissipazione, dunque: \(P_{IRR} = P_{IN}\).
Lo spazio libero é una regione dello spazio assimilabile al vuoto, questo spazio é un mezzo isotropo in cui le onde elettromagnetiche viaggiano in linea retta alla velocitá della luce, ossia a:
$$ \Large\textsf{} c \approx 3 * 10^8 \space \dfrac{m}{s} $$
Nello spazio libero l’intensitá del campo elettrico \(E\), l’intensitá del campo magnetico \(H\) e la densitá di potenza \(S\) possono essere considerati come tensione, corrente e potenza di un circuito elettrico.
Ecco una tabella che chiarisce le associazioni dei valori nello spazio libero e in un circuito elettrico:
| Valori nello Spazio Libero | Valori in un Circuito Elettrico | |
|---|---|---|
| Intensitá del campo elettrico E | = | Tensione V |
| Intesitá del campo magnetico H | = | Corrente I |
| Densitá di potenza S | = | Potenza P |
Inoltre lo spazio libero é considerabile come un mezzo trasmissivo avente impedenza caratteristica:
$$ \Large\textsf{} Z_0 = 120 \pi \space \approx \space 377Ω $$
É possibile estendere le leggi fondamentali dell’elettrotecnica per determinare i legami fra \(E\), \(H\), \(S\). Avendo fatto in precedenza quelle associazioni tra i valori del campo elettromagnetico e grandezze elettriche possiamo definire le seguenti relazioni:
$$ \Large\textsf{} E = Z_0 * H; \space\space S = E * H; \space\space Z_0 = \dfrac{E}{H}; $$
Da questi si possono definire i seguenti legami tra campo elettrico \(E\) e densitá di potenza:
$$ \Large\textsf{} S = \dfrac{E^2}{Z_0} \implies S = \dfrac{E^2}{120 * \pi} [ \space W / m^2 \space] E = \sqrt{S * Z_0} \implies E = \sqrt{S * 120 * \pi} \space\space [\space V / m \space] $$
Intensitá del campo elettromagnetico prodotto da un’antenna isotropica⌗
Lo studio della determinazione del campo elettromagnetico nel caso di un antenna isotropica posta nello spazio libero é di particolare importanza in quanto le formule ricavate possono essere riutilizzate per una valutazione del campo elettromagnetico in un ambiente reale.
Pensiamo dunque al caso ideale di un’antenna trasmittente isotropica posta nello spazio libero. All’antenna viene fornita in ingresso una certa potenza di segnale \(P_{IN}\), che viene totalmente irradiata in modo uniforme in tutte le direzioni, si ha dunque \(P_{IN_ISO} = P_{IRR_ISO}\).
Cos’é la densitá di potenza⌗
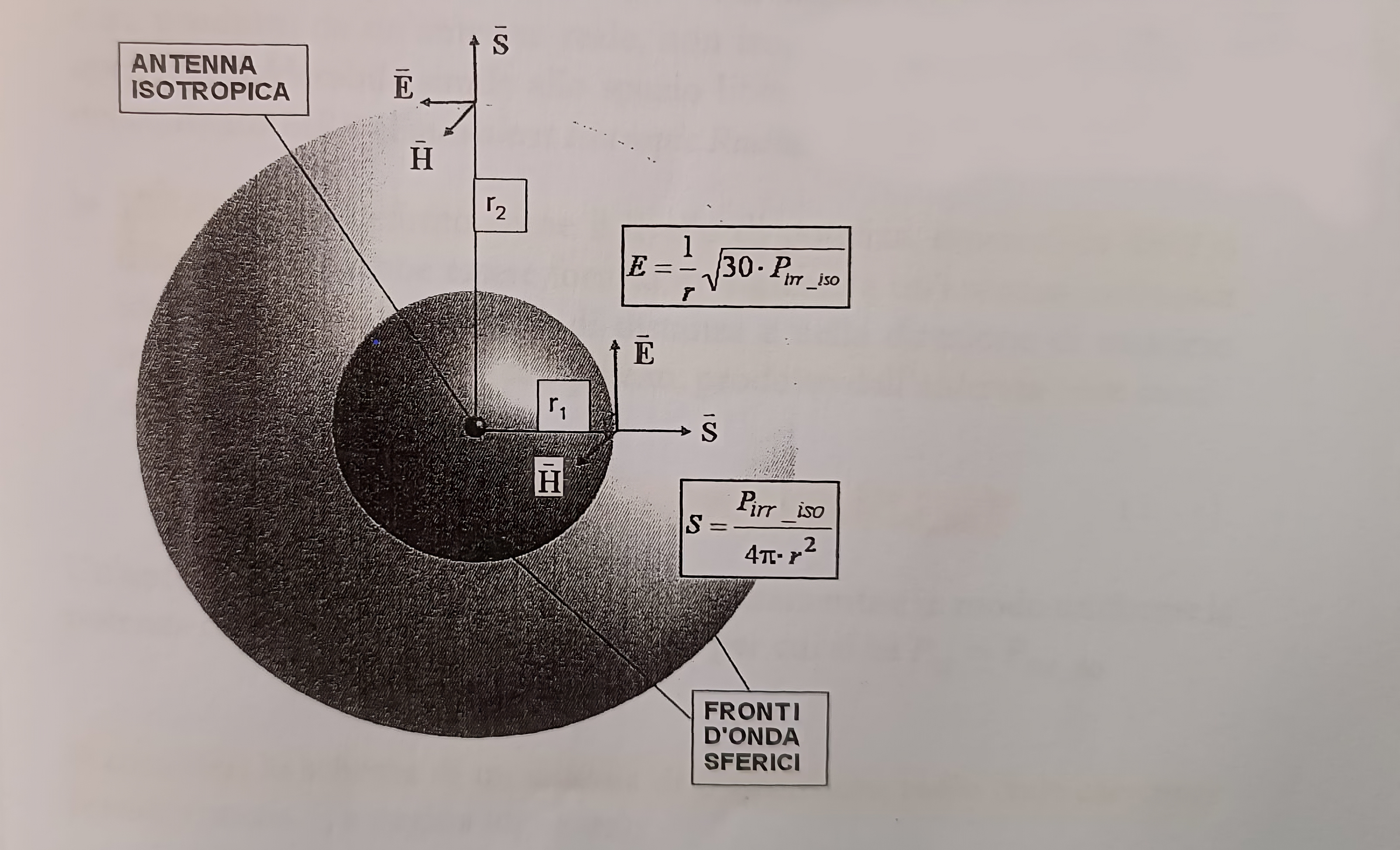
Un generatore a radiofrequenza connesso a un’antenna isotropica, posta nello spazio libero, genererebbe onde elettromagnetiche i cui fronti d’onda sono costituiti da superfici sferiche, in quanto l’irradiazione é uniforme in tutte le direzioni e non si hanno né ostacoli né eterogeneitá.
La densitá di potenza é data dalla potenza per unitá di area:
$$ \Large\textsf{} S = \dfrac{P_{IRR_ISO}}{4\pi * r^2} \space\space [\space \dfrac{W}{m^2} \space] $$
dove:
- \(S \space(W / m^2):\) densitá di potenza a distanza $r$ dall’antenna isotropica ideale;
- \(P_{IRR_ISO} \space (W):\) potenza irradiata in modo isotropico, pari alla potenza di ingresso nel caso di antenna isotropica ideale;
- \(r(m):\) distanza fra l’antenna isotropica e il punto in cui si valuta la densitá di potenza
Cos’é intesitá del campo elettrico⌗
Il valore efficace dell’intensitá del campo elettrico \(E\), si puó calcolare con la relazione:
$$ \Large\textsf{} E = \dfrac{1}{r} \space \sqrt{30 * P_{IRR_ISO_[w]}} \space [\space V/m\space] $$
Ecco un’immagine del campo elettromagnetico generato da un’antenna isotropica:
EIRP e calcolo del campo elettromagnetico prodotto da un’antenna non isotropica⌗
L’EIRP (Effective Isotropic Radiated Power) é definito come il livello di potenza, espresso in dBW o dBm fornito in ingresso a un’antenna isotropica per fornire lo stesso campo elettromagnetico prodotto dall’antenna reale:
$$ \Large\textsf{} EIRP = 10 \log_{10}(P_{IN_ISO}) = 10 \log_{10}(P_{IRR_ISO}) $$
In altre parole dunque, l’EIRP descrivere la potenza totale irradiata da un’antenna in una determinata direzione, rispetto alla potenza che sarebbe irradiata se l’antenna fosse una sorgente isotropica ideale che irradia uniformemente in tutte le direzioni.
L’EIRP tiene conto della potenza di trasmissione dell’antenna e della direzionalità del diagramma di radiazione dell’antenna stessa e tiene conto del fatto che un’antenna non irradia uniformemente in tutte le direzioni ma concentra la potenza in determinate direzioni. Infine l’EIRP viene utilizzata per rappresentare una misura della capacità dell’antenna di trasmettere segnali a lunghe distanze.
Calcolo dell’EIRP⌗
In precedenza abbiamo visto la formula generica per il calcolo dell’EIRP, ma esiste anche un’altra circostanza nella quale va calcolato. Si consideri lo schema di un sistema di trasmissione radio reale che comprenda:
- Un trasmettitore con un segnale che ha una certa potenza \(P_{TX} (W)\) e un livello di potenza \(L_{PTX} = 10\log(P_{TX_[W]})\) dBW.
- Un cavo che collega il trasmettitore all’antenna con un’attenuazione \(A_F(dB)\)
- Un’antenna trasmittente con un guadagno \(G_{ant} (dB)\)
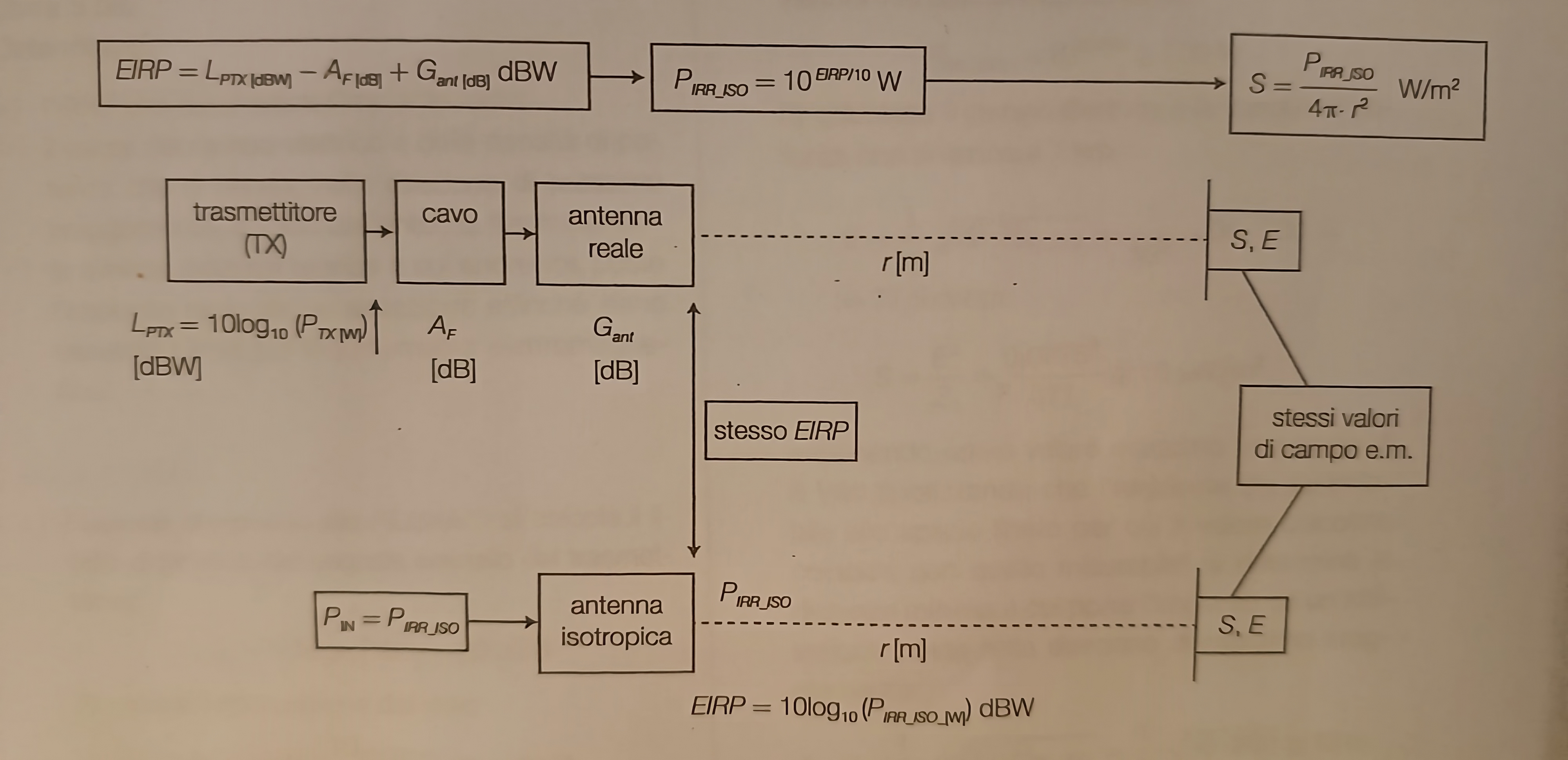
L’EIRP viene calcolato utilizzando i decibel:
$$ \Large\textsf{} EIRP = L_{PTX_[dBW]} \space-\space A_{F_[dB]} \space+\space G_{ant_[dB]} \space[dBW] $$
Noto l’EIRP é possibile calcolare la potenza equivalente che dovrebbe irradiare un’antenna isotropica per produrre lo stesso campo elettromagnetico che produce l’antenna reale:
$$ \Large\textsf{} P_{IRR_ISO} = 10^{EIRP/10} \space [W] $$
Calcolo del campo elettromagnetico prodotto da un’antenna reale⌗
Nel caso di antenna reale i valori di densitá di potenza (\(S\) e di campo elettrico (\(E\) possono essere calcolati con il seguente procedimento:
- Si calcola l’EIRP.
- Si calcola la potenza equivalente irradiata isotropicamente.
- Si calcolano i valori di \(S\) ed \(E\) con la formula:
$$ \Large\textsf{} S = \dfrac{P_{IRR_ISO}}{4\pi * r^2} \space[W/m^2]; \space\space E = \dfrac{1}{r} * \sqrt{30 * {P_{IRR_ISO}}}\space[W/m]; $$
Il calcolo del campo elettromagnetico in un sistema trasmittente via radio viene effettuato per due motivi:
- Verificare che la sua intensitá sia tale da fornite al ricevitore un segnale avente un livello di potenza sufficiente
- Verificare che il campo elettrico \(E\) misurato e la densitá di potenza \(S\) non debbano superare i seguenti valori:
$$ \Large\textsf{} E_{MAX} \leq 6 \space V/m, \space\space per \space\space 100kHz \leq f \leq 300 GHz \newline S_{MAX} \leq 0,1 \space W/m^2, \space\space per \space\space 3MHz \leq f \leq 300 GHz $$
Le Antenne⌗
L’antenna é l’ultimo elemento di un sistema di trasmissione via radio. Essa riceve un segnale da un trasmettitore il quale imprime su un segnale a radiofrequenza (RF) le informazioni da trasmettere via radio.
L’uscira dell’amplificatore di potenza é un segnale in corrente avente frequenza adatta alla trasmissione via radio e potenza sufficiente a garantire una corretta ricezione.
Dunque possiamo dire che: Un’antenna é definita come un trasduttore che in trasmissione converte un segnale elettrico a radiofrequenza in onde elettromagnetiche irradiate nelle direzioni desiderate, mentre in ricezione converte in modo efficiente le onde elettromagneitche in un segnale elettrico a RF.
Possiamo avere molti tipi di trasmissione radio:
- Radiodiffusione AM ed FM
- TV
- Ponti Radio
- Sistemi cellulari
e i requisiti richiesti per le antenne possono essere diversi. Per esempio la radiodiffusione l’antenna trasmittente é omnidirezionale sul piano orizzontale per poter raggiungere tutti gli utenti, mentre per un collegamento in ponte radio si richiede che l’antenna sia estremamente direttiva cosí da limitare la potenza necessaria per trasmettere.
Per le antenne vale il principio di reciprocitá che afferma: le proprietá di un’antenna rimangono le stesse sia che essa venga usata come antenna trasmittente sia che ricevente.
Teorema di Reciprocitá⌗
Il teorema di reciprocità nelle antenne di telecomunicazione è un principio fondamentale che riguarda la simmetria e l’omogeneità del mezzo di propagazione delle onde elettromagnetiche. In parole semplici, questo teorema afferma che le caratteristiche di trasmissione e di ricezione di un’antenna sono identiche quando viene utilizzata come trasmettitore e come ricevitore.
In altre parole, se un’antenna trasmette un segnale in una determinata direzione e successivamente viene utilizzata per ricevere un segnale nella stessa direzione, le sue proprietà di ricezione saranno le stesse che se fosse stata progettata specificamente per ricevere il segnale in questione. Questo significa che le antenne possono essere utilizzate per la trasmissione e la ricezione di segnali senza necessità di modifiche significative alla loro struttura o alla loro geometria.
Il teorema di reciprocità si applica a tutte le antenne che soddisfano determinate condizioni di simmetria e linearità. In particolare, si applica alle antenne a filo, alle antenne a dipolo, alle antenne a cornetta, alle antenne a riflettore parabolico e alle antenne a schiera. In genere, tutte le antenne che presentano un’impedenza di radiazione costante e omogenea in tutte le direzioni sono compatibili con il teorema di reciprocità.
L’importanza del teorema di reciprocità sta nella sua applicazione pratica. Ad esempio, quando si progetta un sistema di telecomunicazioni, spesso si utilizzano antenne diverse per la trasmissione e la ricezione dei segnali. Tuttavia, grazie al teorema di reciprocità, è possibile utilizzare la stessa antenna sia per trasmettere che per ricevere il segnale, semplificando notevolmente il progetto del sistema e riducendo i costi.
Inoltre, il teorema di reciprocità può essere utilizzato per calcolare l’efficienza di una antenna quando viene utilizzata come ricevitore, poiché l’efficienza di trasmissione e di ricezione sono uguali. Questo può essere utile per determinare la capacità di una antenna di ricevere un segnale in presenza di rumore o interferenze.
In sintesi, il teorema di reciprocità è un principio fondamentale delle antenne di telecomunicazione che permette di semplificare il progetto dei sistemi di comunicazione e di calcolare l’efficienza delle antenne quando vengono utilizzate come ricevitori.
Componenti di un sistema di antenna⌗
Un impianto di trasmissione e/o ricezione via radio comprende un sistema di antenna, il quale puó essere costituito dai seguenti elementi:
- Antenna: é l’elemento irradiante o ricevente, puó essere montata su una torre (che prende il nome di traliccio o palo) al fine di garantire la copertura radio alla distanza massima prevista per il sistema di comunicazione via radio.
- Linea di trasmissione (feeder d’antenna): é utilizzata per collegare il trasmettitore (o il ricevitore) con l’antenna. Ha lo scopo di trasferire il segnale dal trasmettitore all’antenna con la minima attenuazione possibile.
- Dispositivo di adattamento: consente di riprisitnare l’adattamento fra linea e antenna nel caso in cui l’impedenza dell’antenna non si auguale all’impedenza caratteristica della linea.
- Dispositivo di separazione TX-RX (duplexer o circolatore): é utilizzato per separare i sensi di trasmissione (TX) e ricezione (RX) nel caso in cui si utilizzi la stessa antenna sia per trasmettere sia per ricevere.
- Dispositivi ausiliari: sono necessari nei grandi impianti per segnalare la presenza dell’antenna, per la protezione contro il ghiaccio, il vento e l’acqua, per il puntamento dell’antenna nel caso di antenne direttive.
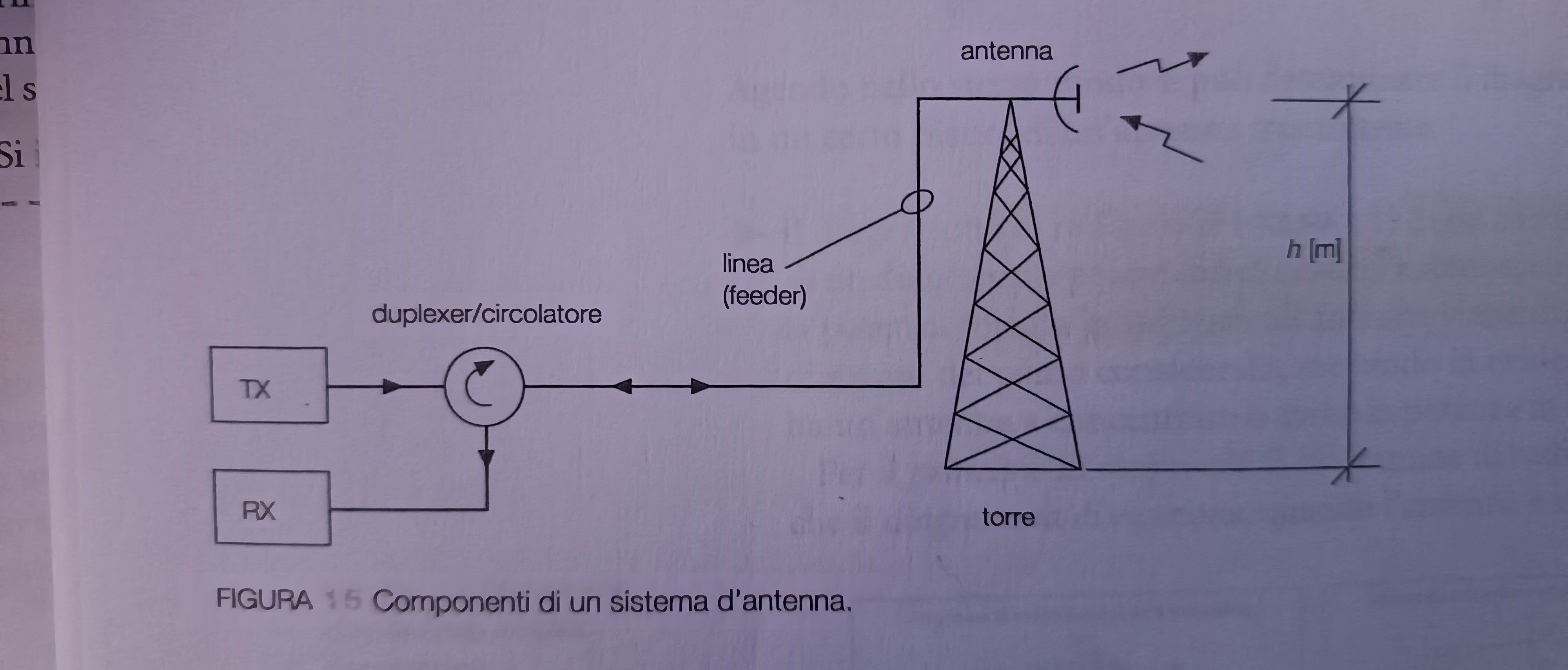
Diagramma di radiazione e solido di radiazione⌗
Per rappresentare le direzioni preferenziali in cui irradia un’antenna si utilizza un diagramma di radiazione (radiation pattern).
Un antenna reale, non irradia in modo uniforme in tutte le direzioni dello spazio. Questo diagramma mette bene in evidenza l’attitudine che ha una sorgente a concetrare la potenza in certe direzioni e quindi ne evidenzia il grado di direttività:
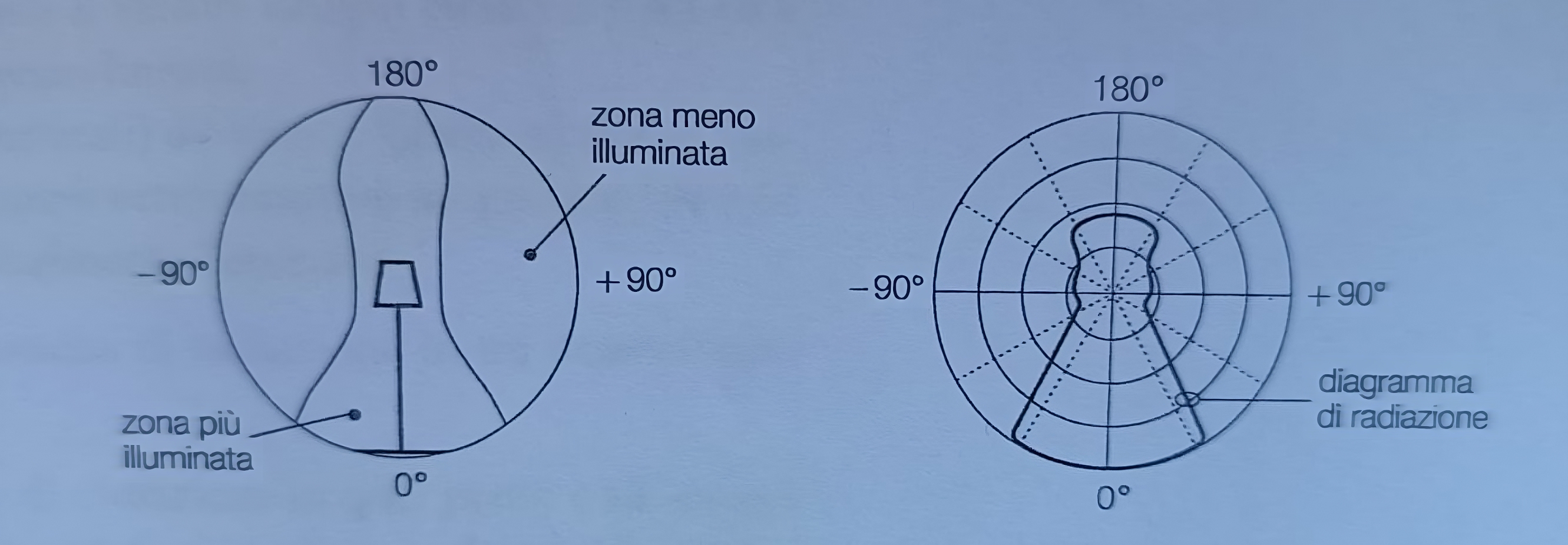
Il diagramma di radiazione è una curva, riportata di solito su un diagramma polare con al centro l’antenna, che rappresenta come la potenza fornita in ingresso all’antenna viene distribuita nella varie direzione del piano considerato.
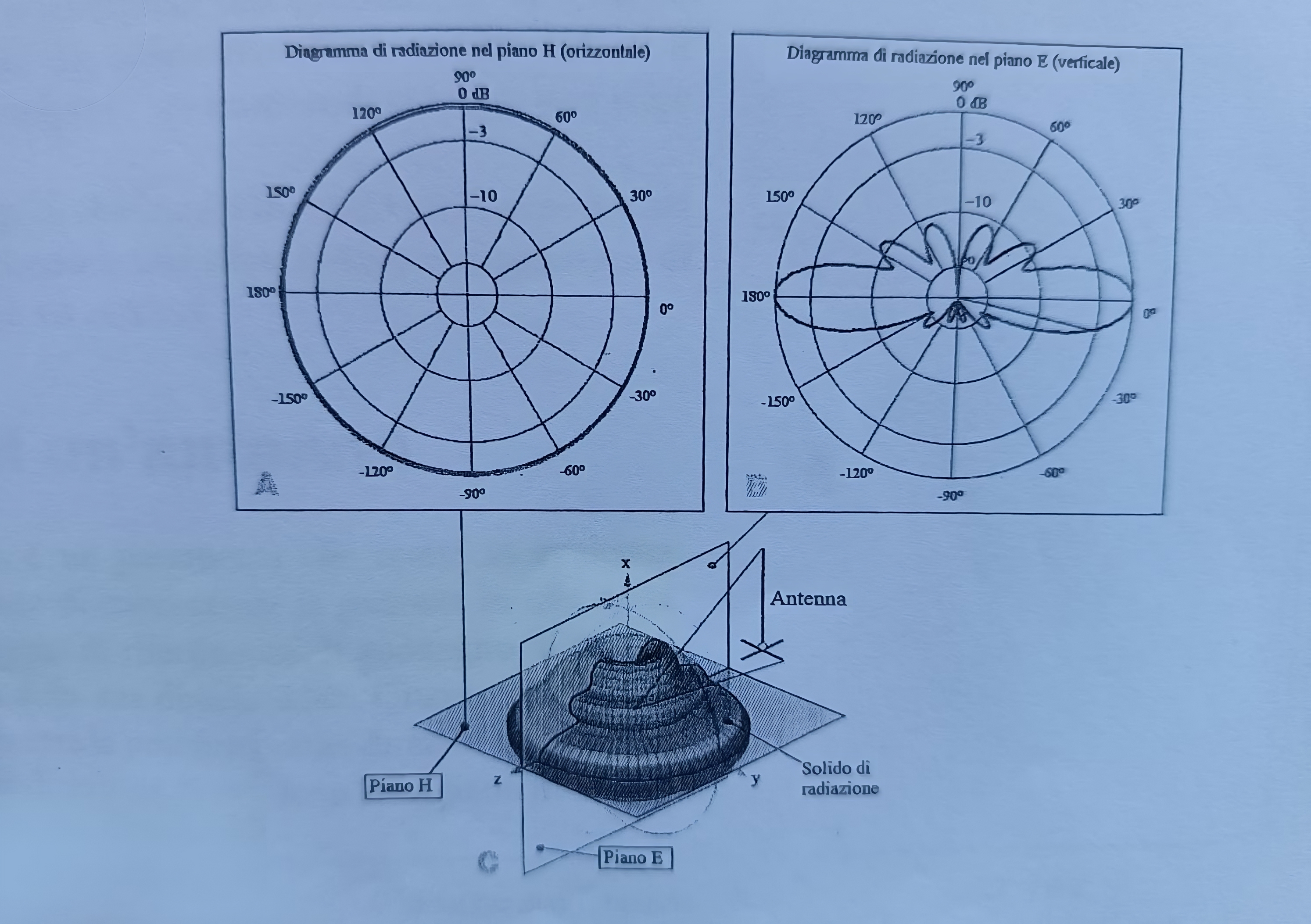
Il diagramma di radiazione può riportare i valori del guadagno che l’antenna presenta nelle varie direzioni del piano considerato, espressi in decibel.
Normalmente si tracciano i diagrammi di radiazione in due piani tra loro ortogonali denominati:
- Piano verticale o piano E: è il piano in cui giace il vettore campo elettrico E ed è anche il piano su cui giace un’antenna lineare;
- Piano orizzontale o piano H: è il piano in cui giace il vettore campo magnetico H ed è anche il piano che taglia ortogonalmente l’antenna;
A seconda di come è fatto il diagramma di radiazione in un determinato piano, un’antenna viene definita:
- Omnidirezionale: se il diagramma di radiazione in quel piano è all’incirca un cerchio l’antenna irradia uniformemente in tutte le direzioni;
- Direttiva: se il diagramma di radiazione in quel piano presenta delle direzioni prefenziali di irraggiamento
- Direttiva unidirezionale: se il diagramma di radiazione mostra una direzione preferenziale di irragiamento, quella anteriore data dal lobo principale del diagramma. Altre direzioni di minore irraggiamento, non desiderate, definite dai lobi secondari del diagramma di radiazione.
Guadagno di un’antenna⌗
Il guadagno di un’antenna è un parametro che mette in evidenza quanto un’antenna può concentrare la potenza in una certa direzione rispetto a un’antenna di riferimento. Il guadagno di un’antenna è direttiva tanto più alto è il suo guadagno.
A seconda dell’impiego si possono avere due antenne di riferimento:
- Antenna isotropa: un’antenna puramente ideale, che irradia in modo uniforme in tutte le direzioni.
- Dipolo in \(\lambda /2\): viene utilizzata come riferimento per le antenne lineari, in particolare nel settore delle antenne riceveneti TV.
Guadagno rispetto all’antenna isotropica⌗
Il guadagno di un’antenna può essere definito come il rapporto fra la potenza che è necessaria dare in ingresso a un’antenna isotropica ideale è la potenza che è necessario fornire al connettore dell’antenna in esame.
Il guadagno rispetto all’antenna isotropica si calcola come:
$$ \Large\textsf{} G = 10\log_{10} \space \dfrac{P_{ISO}}{P_{IN}} \space [dBi] $$
Il guadagno viene espresso in \(dBi\) per indicare che è stato ottenuto prendendo come riferimento l’antenna isotropica ideale (i = isotropica).
Il guadagno di un’antenna esprime l’aumento della potenza irradiata che si ottiene concentrando la potenza in certe direzioni.
Il valore del guadagno nelle altre direzioni, denominato guadagno direttivo, può essere fornito tramite un diagramma di radiazione in cui si riporta il guadagno per i diversi angoli.
Quando il guadagno viene espresso semplicemente in \(dB\) risulta sottointeso che l’antenna di riferimento è quella isotropa anche se non si mette.
Noto il guadagno è possibile calcolare il livello con cui dovrebbe irradiare un’antenna per produrre lo stesso campo dell’antenna in considerazione:
$$ \Large\textsf{} G_{[dB]} = 10\log_{10} \space P_{ISO} - 10\log_{10} \space P_{IN} = EIRP - L_{P_IN} $$
Da cui si ottiene la seguente formula inversa:
$$ \Large\textsf{} EIRP = L_{P_IN} \space + \space G_{dB} $$
Se non è noto il livello di potenza in ingresso all’antenna ( \(L_{P_IN}\) ), è possibile calcolarlo in funzione del livello di potenza del trasmettitore ( \(L_{P_TX}\) ) e dell’attenuazione della linea (feeder, \(A_F\)) come:
$$ \Large\textsf{} L_{P_IN} = L_{P_TX} - A_F $$
La direttivitá \(D\) il rapporto tra la potenza che dovrebbe irradiare un’antenna isotropica ( \(P_{ISO}\) ) e la potenza irradiata ( \(P_{IRR}\) ) dall’antenna in esame affinche il campo da loro prodotto sia lo stesso:
$$ \Large\textsf{} D = 10\log_{10} \space \dfrac{P_{ISO}}{P_{IRR}} \space [dBi] $$
Il guadagno effettivo (\(G\)), detto anche guadagno di potenza, é minore della direttivitá (\(G < D\)) a causa del fatto che un’antenna reale causa una piccola dissipazione di potenza, per cui la potenza irradiata é inferiore rispetto alla potenza in ingresso.
Guadagno rispetto all’antenna al dipolo in λ/2⌗
Il guadagno viene espresso in \(dBd\) quando si prende come antenna di riferimento il dipolo \(\lambda/2\), il pedice $d$ sta proprio a indicare che si é presa come antenna di riferimento il dipolo in \(\lambda/2\).
Principali tipi di antenne⌗
È possibile identificare due categorie principali:
-
Antenne lineari: esse sono omnidirezionali a banda larga, direttive;
-
Antenna a dipolo: un dipolo è un’antenna costituita da due elementi conduttori che sono allineati elettricamente, ma con polarità opposta. Il dipolo è un’antenna molto comune e può essere utilizzato in molte applicazioni wireless, come le trasmissioni radio e televisive.
Il dipolo è solitamente costituito da un filo metallico sottile che viene tagliato a una lunghezza specifica in base alla frequenza di trasmissione desiderata. Quando il dipolo viene alimentato con un segnale di frequenza corrispondente alla sua lunghezza, le correnti elettriche fluiscono attraverso i suoi elementi, creando un campo elettromagnetico che si irradia nell’ambiente circostante.
Il dipolo è una delle antenne più semplici e convenienti da costruire, ed è spesso utilizzato come riferimento per la valutazione di altre antenne più complesse. Il dipolo può anche essere utilizzato in combinazione con altri elementi per creare antenne più direzionali o per migliorare le prestazioni in determinate direzioni.
-
-
Antenne a superficie: esse sono antenne direttive con alto guadagno; tra esse la più diffusa è l’antenna a parabola;
Principio di funzionamento delle antenne lineari⌗
Consideriamo un tronco di linea bifilare con terminazione aperta alimentato da un generatore a radiofrequenza ($RF$). Su di esso si viene ad instaurare un regime di onde stazionarie di corrente e tensione. Questa linea irradia poco per due motivi:
- I due conduttori sono vicini e per questo motivio l’irradiazione di uno di essi cancella quella dell’altro.
- Se si considera lo spazio come un carico esso risulta fortemente disadattato e così si ha poco trasferimento di potenza a essa.
Se però si piegano a $90\degree$gradi le estremità della linea, le correnti avranno lo stesso verso in questo tratto e sarà quindi possibile irradiare energia nello spazio in modo efficiente. In questo modo si ottiene un antenna denominata antenna a dipolo o antenna Hertziana.
Dunque in sintesi: Se si vuole massimizzare l’irradiazione è necessario piegare i coduttori a una distanza \(\lambda/4\) dall’estremità ottenendo così un’antenna lunga \(\lambda/2\), denominata per questo dipolo \(\lambda/2\) o dipolo a mezz’onda.
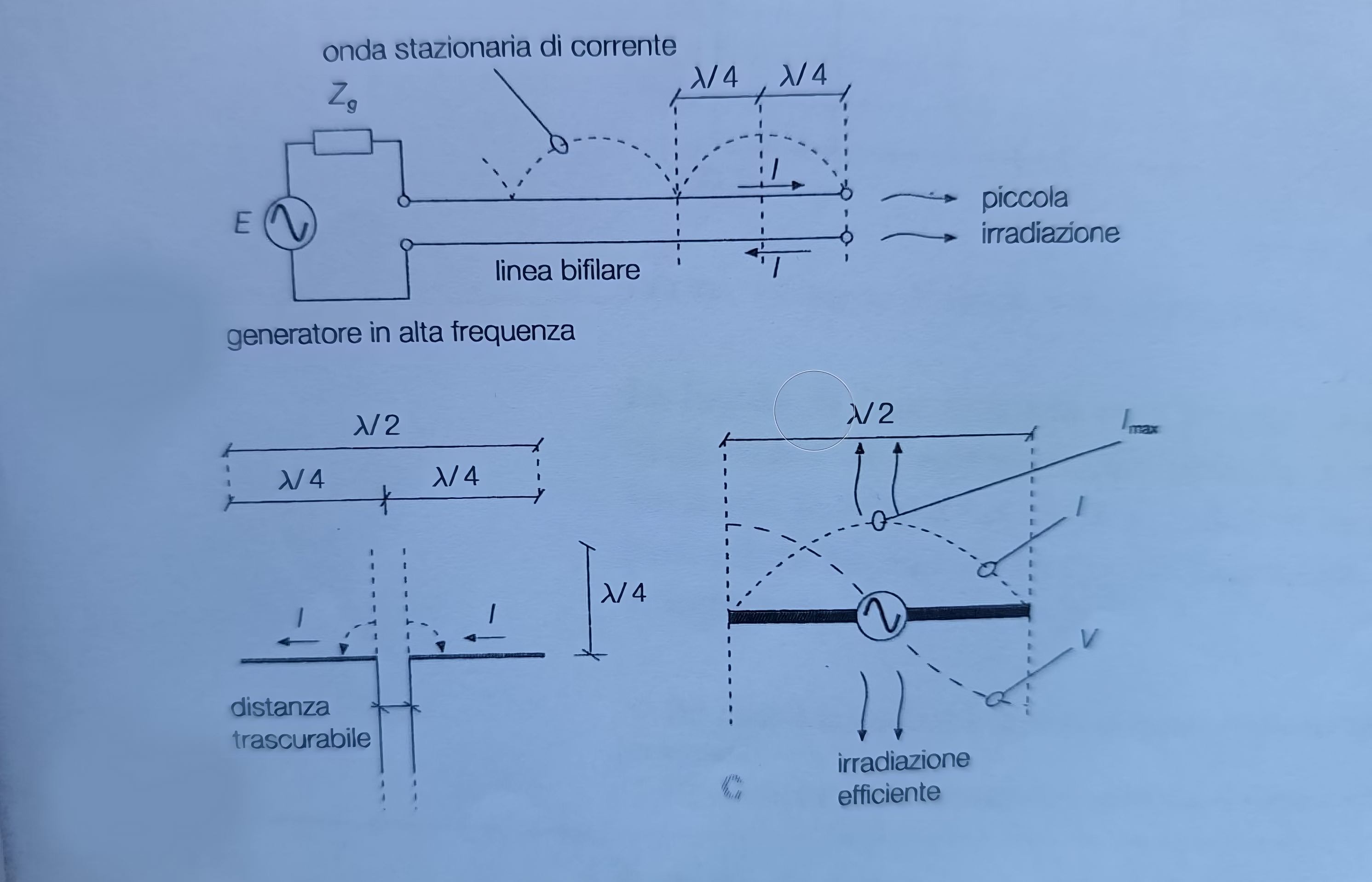
Il dipolo \(\lambda/2\) , ha un comportamento simile a quello di un tronco di linea in \(\lambda/4\); l’onda stazionaria di corrente presenta un minimo alle estremità, mentre è massimo al centro.
Banda di un’antenna lineare⌗
Un’antenna lineare, a dipolo, ha un comportamento analogo a quello di un circuito risonante.
La banda (\(B\)) di un’antenna può essere defnita come l’intervallo di frequenza entro cui il ROS si mantiene entro dei limiti. Tipicamente i valori limite di ROS sono compresi tra \(1,5\) e \(2\).
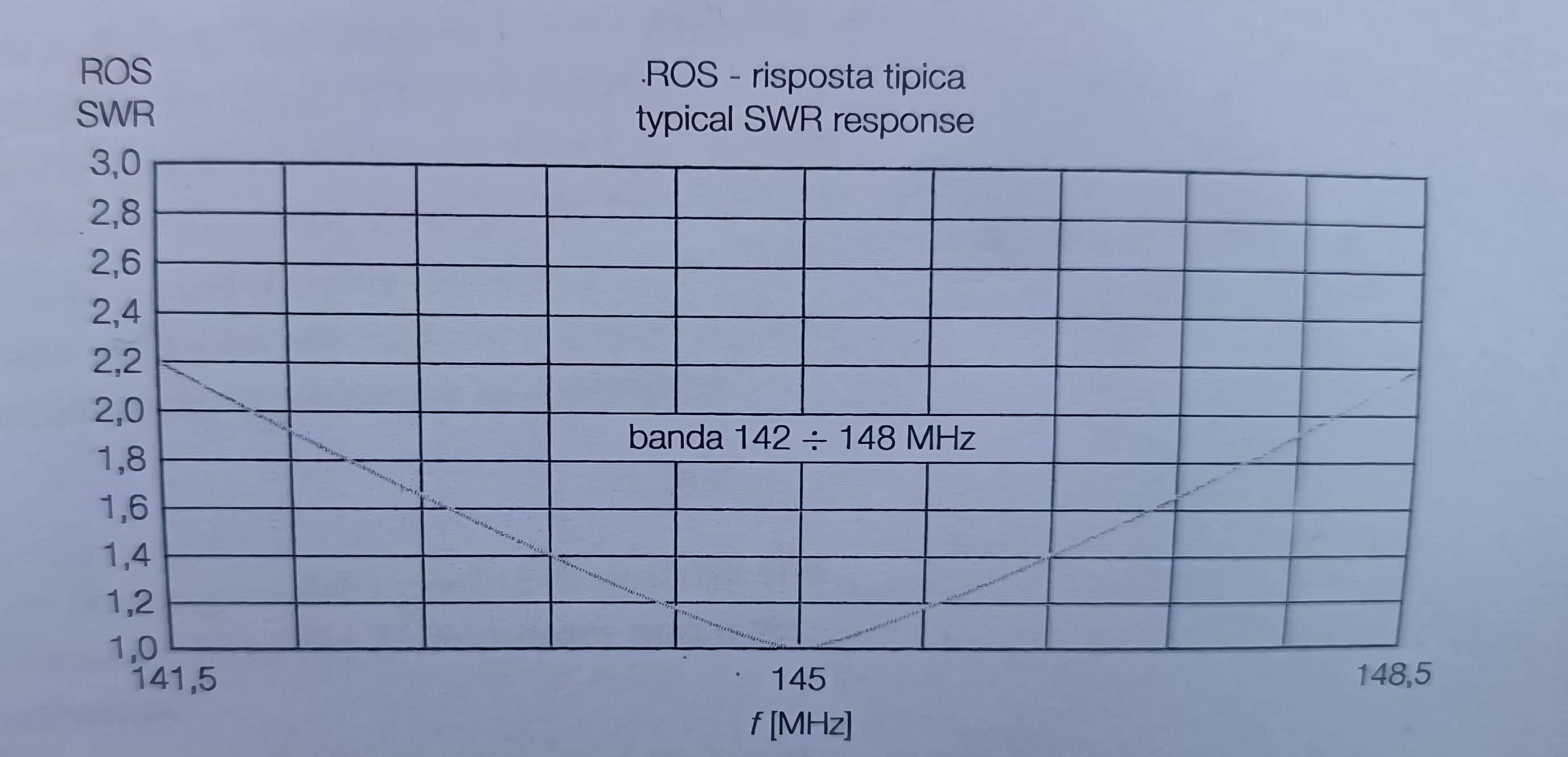
La banda di una antenna è in pratica l’intervallo di frequenza in cui il diagramma di radiazione dell’antenna fornisce le prestazioni richieste.
La banda dipende dal diametro del conduttore con il quale si realizza l’antenna.
Resistenza d’antenna⌗
Un’antenna rappresenta per la linea (feeder) un carico che é resistivo in risonanza e viene denominato resistenza d’antenna ( \(R_a\) ). La resistenza d’antenna viene considerata come la somma di due resistenze:
- La resistenza di radiazione ( \(R_r\) )
- La resistenza di dissipazione (\( R_d\) )
$$ \Large\textsf{} R_a \space = \space R_r \space + \space R_d \space [Ω] $$
Resistenza di radiazione⌗
La resistenza di radiazione é definita come il rapporto tra la potenza irradiata dall’antenna ( \(P_{IRR}\) ) e il quadrato della corrente ( \(I_{IN}\) ) che giunge in ingresso all’antenna (punto di alimentazione):
$$ \Large\textsf{} R_r = \dfrac{P_{IRR}}{I^2_{IN}} \space [Ω] $$
La resistenza di radiazione é quella resistenza che dissipa una potenza pari a quella irradiata dall’antenna. Per un dipolo la \(R_r\) dipende da diversi fattori, tra i quali:
- Diametro del conduttore: la \(R_r\) aumenta al diminuire del diametro del coduttore
- Altezza dal suolo: alla quale si pone l’antenna; le onde elettromagnetiche emesse dall’antenna possono venire riflesse dalla terra ed indurre una corrente nell’antenna. A seconda della distanza percorsa varia la fase della corrente indotta e quindi varia la corrente totale. Si modifica percío anche la resistenza di radiazione
Resistenza di dissipazione⌗
La resistenza di dissipazione tiene conto della perdita di potenza che si puó avere sull’antenna. Per valutare le perdite sull’antenna si definie il rendimento ( \(\eta\) ) dato dal rapporto fra la potenza irradiata ( \(P_{IRR}\) ) e la potenza in ingresso all’antenna ( \(P_{IN}\) ):
$$ \Large\textsf{}\eta = \dfrac{P_{IRR}}{P_{IN}} = \dfrac{R_r}{R_r + R_d} $$
Parametri tipi di delle antenne riceventi⌗
In risonanza un’antenna ricevente puó essere considerata come un generatore avente resistenza interna \(R_a\), in grado di erogare una certa tensione e una certa potenza a un carico \(R_u\):
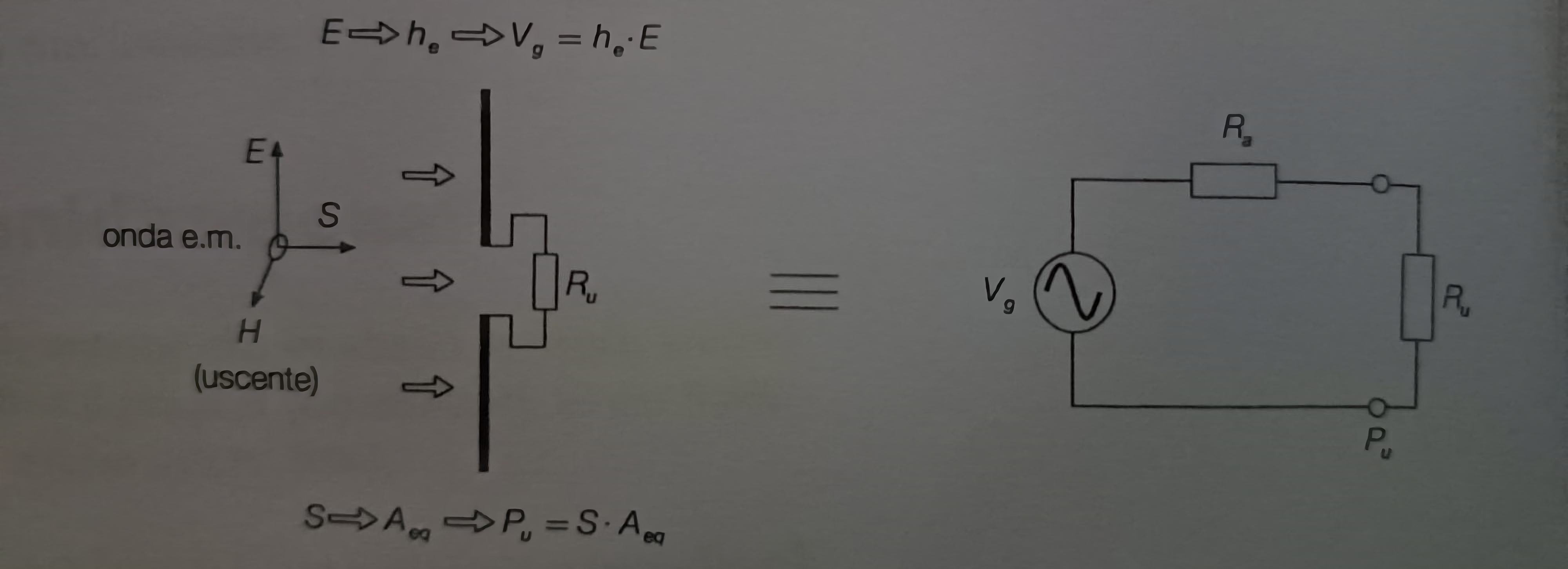
Supponendo che l’antenna sia adattata e correttamente orientata, la tensione e la potenza che essa é in grado di erogare dipendono da due parametri di traduzione, ossia:
- L’altezza efficace ( \(h\) )
- L’area equivalente ( \(A_{eq} \))
Altezza efficace⌗
L’altezza efficace \(h_e\) è un termine utilizzato in telecomunicazioni per descrivere l’altezza a cui un’antenna appare “efficace” nel trasferimento di segnali radio. In particolare, si riferisce all’altezza a cui un’antenna sembra essere vista dall’altro lato della comunicazione.
Inoltre, l’altezza efficace di un’antenna dipende da diversi fattori, tra cui l’altezza fisica dell’antenna, la frequenza del segnale trasmesso, la presenza di ostacoli o interferenze nell’ambiente circostante e la potenza di trasmissione dell’antenna.
Fattore di traduzione da campo elettrico indicente ( \(E \space V/m\) ) a tensione d’uscita ( \(RMS\) ) a vuoto, \(V_g \space (V)\):
$$ \Large\textsf{}V_g = h_e * E $$
Poiche \(E\) si esprime in \(V/m\), mentre \(V_g\) é in \(V\), \(h_e\) si esprime in mentri. Per le antenna a dipolo l’altezza efficace si puó calcolare come:
$$ \Large\textsf{}h_e = \lambda\sqrt{\dfrac{R_r * G}{\pi * Z_0}} \space [m] $$
Dove:
- \(R_r\): resistenza di radiazione;
- \(G\): guadagno dell’antenna non in db;
- \(Z_0 = 120 \pi\): impedenza caratteristica dello spazio libero;
- \(\lambda\): lunghezza d’onda dell’onda elettromagnetica indicente;
Fattore di traduzione da campo elettrico indicente⌗
Il fattore di traduzione da campo elettrico, noto anche come coefficiente di accoppiamento o fattore di accoppiamento, è un parametro che indica la quantità di energia elettromagnetica trasmessa da un’antenna trasmittente ad un’antenna ricevente.
In particolare, il fattore di traduzione da campo elettrico misura la frazione del campo elettrico irradiato dalla prima antenna che viene ricevuta efficacemente dalla seconda antenna, tenendo conto delle caratteristiche geometriche e di orientamento delle due antenne, della distanza tra di esse e delle proprietà del mezzo di propagazione.
In pratica, il fattore di traduzione da campo elettrico è un parametro importante per la progettazione e l’ottimizzazione delle antenne, poiché consente di valutare l’efficacia di un’antenna trasmittente nel trasferire energia ad un’altra antenna ricevente.
Area equivalente⌗
L’area equivalente \(A_{eq}\) è una misura dell’efficienza dell’antenna e rappresenta l’area che l’antenna sembra occupare nell’ambiente circostante in termini di capacità di ricezione o trasmissione del segnale radio.
Fattore di trasduzione da densitá di potenza incidente (\(S\)) a potenza fornita al carico adattato ( \(P_u\) ):
$$ \Large\textsf{}P_u = S * A_q \space [W] $$
Poiché $S$ si esprime in \(W/m^2\), mentre \(P\) é in \(W\), dimensionalmente \(A_{eq}\) si esprime in \(m^2\).
L’area equivalente (\( A_{eq}\) ) di un’antenna si calcome come:
$$ \Large\textsf{}A_{eq} = G \space\dfrac{\lambda^2}{4\pi} \space [m^2] $$
Dove:
- \(G\): guadagno dell’antenna non in dB;
- \( \lambda \): lunghezza d’onda dell’onda elettromagnetica indicente
Correlazione tra Dimensioni dell’antenna e l’area equivalente⌗
La dimensione di un’antenna si riferisce alle sue caratteristiche fisiche, come la lunghezza, il diametro, l’altezza e l’area di apertura. La dimensione dell’antenna è importante perché determina le sue proprietà elettriche, come l’impedenza, la direttività, la polarizzazione e la larghezza di banda. In generale, le antenne più grandi hanno una maggiore direttività e una maggiore efficienza rispetto alle antenne più piccole, ma possono essere più costose e difficili da installare. Tuttavia, le dimensioni dell’antenna dipendono dalle specifiche esigenze di trasmissione e ricezione del sistema di telecomunicazioni in cui viene utilizzata. In telecomunicazioni, l’area equivalente di un’antenna è una misura del suo potere di ricezione o trasmissione, in relazione alla sua area fisica. Essa è definita come l’area di un’antenna ideale che ha lo stesso potere di ricezione o trasmissione dell’antenna reale.
La dimensione dell’antenna è strettamente correlata all’area equivalente dell’antenna. In generale, le antenne più grandi hanno un’area equivalente maggiore rispetto alle antenne più piccole. Ciò significa che le antenne più grandi possono trasmettere o ricevere segnali più potenti rispetto alle antenne più piccole, a parità di condizioni.
Tuttavia, la relazione tra la dimensione e l’area equivalente dell’antenna non è lineare. Ciò significa che raddoppiare la dimensione dell’antenna non raddoppia necessariamente la sua area equivalente. La relazione dipende dalle specifiche caratteristiche dell’antenna, come la sua geometria, la frequenza di lavoro e le proprietà del materiale di cui è fatta. Pertanto, la scelta delle dimensioni dell’antenna dipende dalle specifiche esigenze di trasmissione e ricezione del sistema di telecomunicazioni in cui viene utilizzata, e deve essere fatta in base a una progettazione attenta e un’analisi dettagliata delle caratteristiche dell’antenna.
Nel caso del dipolo l’area equivalente è legata alla lunghezza d’onda, nel caso della parabola è legata al diametro dell’antenna.
Fattore di trasduzione da densitá di potenza incidente⌗
Il fattore di trasduzione da densità di potenza incidente, noto anche come fattore di conversione, è un parametro che indica la capacità di un’antenna ricevente di convertire la densità di potenza del campo elettromagnetico incidente in una tensione elettrica rilevabile ai suoi terminali di uscita.
In altre parole, il fattore di trasduzione da densità di potenza incidente rappresenta il rapporto tra la potenza elettrica generata ai terminali di uscita dell’antenna e la densità di potenza del campo elettromagnetico incidente sull’antenna stessa, espressa in watt per metro quadrato.
Il fattore di trasduzione dipende dalle caratteristiche geometriche e di orientamento dell’antenna ricevente, dalla frequenza del segnale incidente, dalla polarizzazione del segnale elettromagnetico e dalle proprietà del mezzo di propagazione.
Il fattore di trasduzione è un parametro importante per la valutazione delle prestazioni delle antenne riceventi, in quanto consente di stimare l’efficienza con cui l’antenna converte l’energia elettromagnetica incidente in una tensione di uscita utile per l’elaborazione del segnale ricevuto.
Antenne omnidirezionali⌗
Sono omnidirezionali quelle antenne che irradiano in modo uniforme in un piano, che di solito é il piano \(H\) (orizzontale), in cui il diagramma di radiazione é un cerchio.
In altri piani, come per esempio nel piano \(E\) sono direttive.
Le antenne omnidirezionali sono utilizzate quando il sistema di trasmissione si trova in posizione baricentrica rispetto all’area da servire, per cui nel piano \(H\), si ha lo stesso campo indipendentemente dalla posizione dell’antenna ricevente. É questo, il caso della trasmissone in brodcast (da un trasmettitore verso tutti i ricevitori che si trovano entro l’area di copertura) di trasmettitori radio AM/FM e TV.
In questo caso l’antenna fondamentale é il tipolo in \( \lambda/2\). É poi possibile intervenire sulla lunghezza o sulla sezione dell’antenna per modificare il diagramma di radiazione nel piano verticale, in modo da ottenere le caratteristiche desiderate in termini di lunghezza dell’antenna e quindi di praticitá nell’installazione.
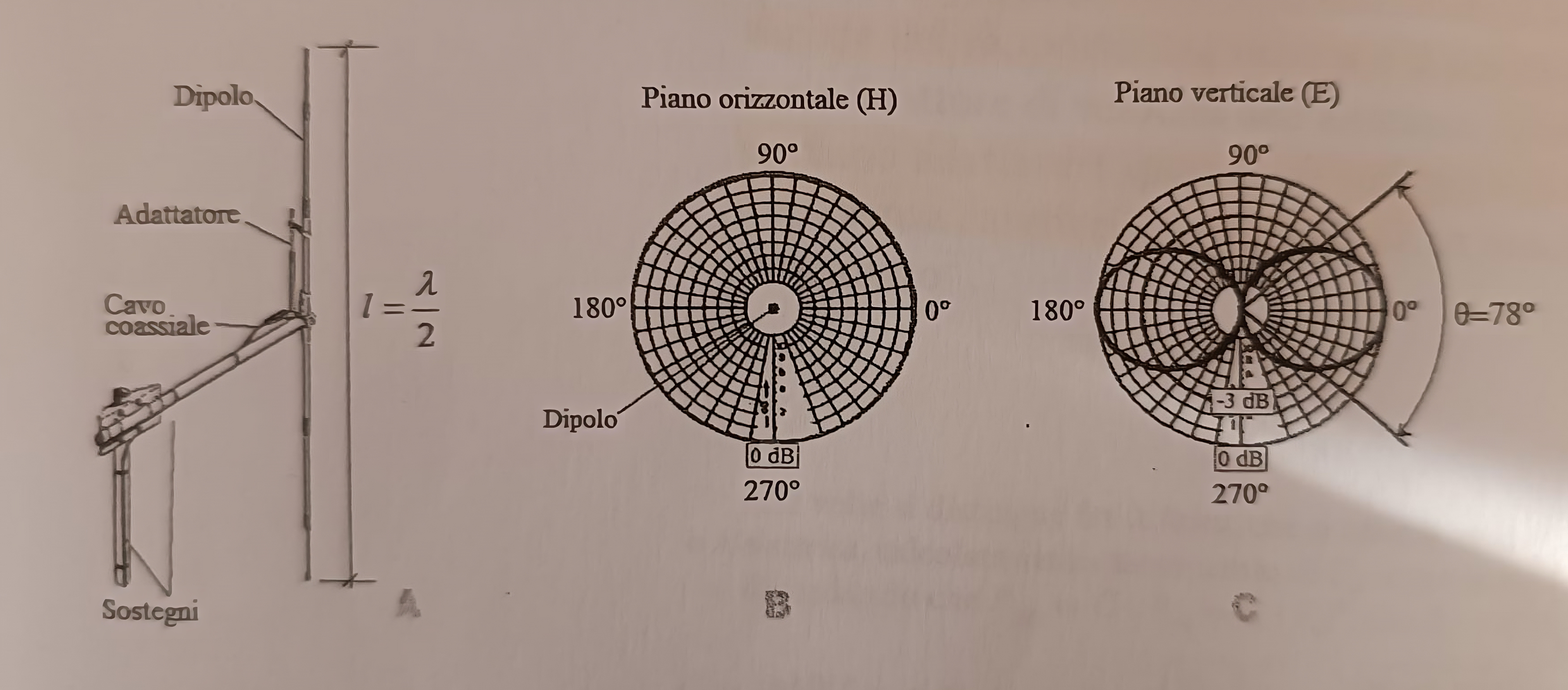
Dipolo in λ/2⌗
E un’antenna a dipolo la cui lunghezza fisica ( \(l\) ) é pari a \( \lambda/2\), dove \( \lambda\) é la lunghezza d’onda del segnale (portante) impresso sull’antenna. Per questo motivio viene chiamato dipolo in \( \lambda/2\) o dipolo a mezz’onda (half wave dipolo). La lunghezza fisica di un dipolo in \( \lambda/2\) si calcola come:
$$ \Large\textsf{}l_{fisica} = \dfrac{\lambda}{2} = \dfrac{1}{2} \frac{F_v * c}{f} \space [m] $$
Dove:
- \(c \approx3 * 10^8 \space m/s\): velocitá di propagazione nel vuoto;
- \(F_v\): fattore di velocitá, tipicamente compreso fra \(0,92\) e \(0,98\);
- \(f\): frequenza (portante) del segnale che deve essere irradiato;
Anche per le antenne si definisce, infatti, un fattore di velocitá (\(F_v\)), quanto la velocitá di propagazione nel conduttore é minore di quella nel vuoto. Le principali caratteristiche di un dipolo \( \lambda/2\) sono le seguenti:
- Il guadagno é pari a \(G = 2,15\) dBi;
- Nel piano \(H\) il diagramma di radiazione é un cerchio e quindi l’antenna é omnidirezionale; nel piano \(H\) l’intensitá del campo elettrico si puó determinare, ricordando la formula:
$$ \Large\textsf{}E = \dfrac{60 * I}{r} \space [V/m] $$
Dove:
- \(I\) (A): corrente nel punto di alimentazione;
- \(r\) (m): distanza dall’antenna;
Le altre caratteristiche:
- nel piano \(E\) l’antenna é direttiva, con un angolo di apertura pari a \( \theta = 78 \degree\);
- Nello spazio libero la resistenza di radiazione teorica é pari a \(R_r = 73 \spaceΩ\); la resistenza d’antenna effettiva, varia al variare del rapporto \( \lambda/d\) dove \(d\) é il diametro del conduttore, spesso, si inserisce un opportuno adattatore quando si collega l’antenna a un cavo coassiale con impedenza caratteristica \(Z_0 = 50 \space Ω\);
Quando la frequenza dei segnali da trasmettere é relativamente bassa la lunghezza fisica di un dipolo \( \lambda/2\) diventa rilevante. Sono state cosí realizzate antenne che consentono di avere lunghezze inferiori, come le seguenti: antenna Marconi o antenna in \( \lambda/4\), Ground Plane, antenne caricate.
Antenna Marconi⌗
L’antenna Marconi (o antenna a \( \lambda/4\) ) é un’antenna che dimezza la lunghezza dell’elemento radiante rispetto al dipolo \( \lambda/2\), essa é montata verticalmente e connessa a terra attraverso il generatore che lo alimenta; questa antenna sfrutta la terra come superficie conduttrice riflettente.
Il suo funzionamento si basa sul principio delle immagini il quale afferma che il campo prodotto da una carica posta nelle vicinanze di un piano conduttore equivale al campo nel caso in cui vi fosse una carica di segno opposto, simmetrica rispetto al piano e detta carica immagine.
É possibile sostituire un semidipolo con un piano conduttore, che puó anche essere il terreno. Supponendo la terra sia un perfetto conduttore, essa produce lo stesso effetto di un semidipolo immagine, e quindi nella porzione di spazio che contiene l’antenna reale si ottiene un diagramma di radiazione analogo a quello di un dipolo \( \lambda/2\).
Le caratteristiche fondamentali di un’antenna \( \lambda/4\) sono:
-
L’antenna é omnidirezionale nel piano \(H\), in cui il diagramma di radiazione é un cerchio;
-
Il diagramma di radiazione nel piano \(E\) é pari alla metá superiore di quello del dipolo \( \lambda/2\);
-
Il guadagno aumenta di \(3 dB\) e diventa pari a:
$$ \Large\textsf{}G = 3 dBd \implies G = 5,15 dBi $$
-
La resistenza di radiazione si dimezza e per un’antenna filiforme diventa pari a \(R_r = 36,5 Ω\), in quanto l’antenna é costituita da un semidipolo.
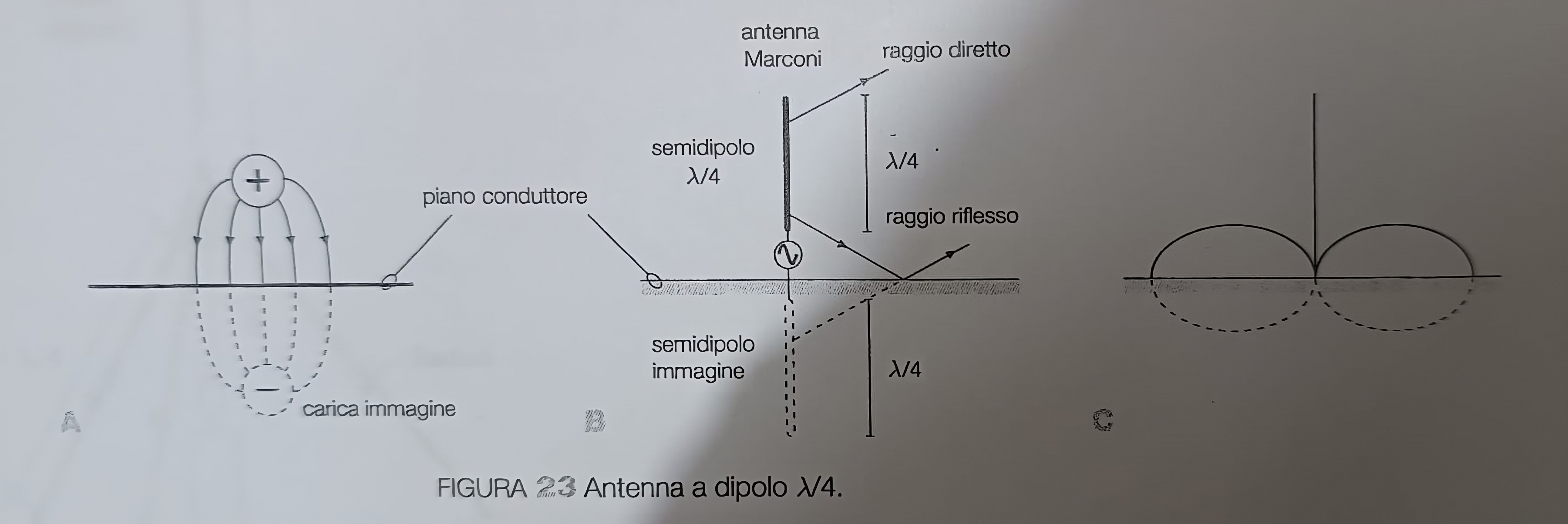
L’antenna Marconi trova impiego prevalentemente nelle trasmissioni a frequenza relativamente bassa, in onde lunghe (LF) e onde medie (MF). Per ottenere un piano conduttore di caratteristiche migliori rispetto alla terra si stende sotto l’antenna, una maglia di fili di rame intrecciati, nota come contrappeso (counterpoise).
Antenna Ground Plane⌗
Un’antenna Ground Plane è un tipo di antenna a dipolo in cui la radiazione avviene grazie all’assenza di una sezione del dipolo, sostituita da un piano di massa o “ground plane”. Questo piano di massa, a forma di piatto o di disco, si trova sotto l’antenna e serve come elemento di ritorno per il segnale radio.
In un’antenna Ground Plane ideale, il piano di massa avrebbe un’impedenza infinita e sarebbe perfettamente orizzontale rispetto all’antenna, formando un angolo di 90 gradi rispetto alla direzione di emissione del segnale. In realtà, tuttavia, il piano di massa ha una resistenza finita e non è mai completamente orizzontale, il che può influire sulle prestazioni dell’antenna.
Per quanto riguarda i valori resistivi, la resistenza del piano di massa dipende dal materiale utilizzato, dalle dimensioni e dalla forma. Solitamente si cerca di utilizzare materiali con alta conduttività, come il rame o l’alluminio, per minimizzare la resistenza. Tuttavia, la resistenza del piano di massa può comunque variare a seconda delle condizioni ambientali, come la presenza di umidità o di contaminanti.
L’angolo formato dal piano di massa dipende dalla geometria dell’antenna e dalle esigenze di progetto. In generale, l’angolo deve essere tale da massimizzare il guadagno dell’antenna nella direzione di emissione del segnale e minimizzare il guadagno nelle direzioni indesiderate. Solitamente, l’angolo varia tra i 30 e i 60 gradi rispetto all’orizzontale.
Antenne Caricate⌗
Le antenne caricate sono antenne che utilizzano un’induttanza o un condensatore per modificare le loro proprietà elettriche, in modo da adattarsi meglio alle specifiche esigenze di progetto. La carica, che è una reattanza, può essere utilizzata per vari scopi, come la riduzione delle dimensioni dell’antenna, la regolazione dell’impedenza di ingresso o la focalizzazione della radiazione in determinate direzioni.
Ad esempio, un’antenna a filo rettilineo lunga a λ/4 può essere carica in modo da apparire come un’antenna più corta, ma con le stesse proprietà elettriche. Ciò consente di ottenere una riduzione delle dimensioni fisiche dell’antenna, senza comprometterne le prestazioni.
Inoltre, le antenne caricate possono essere utilizzate per adattare l’impedenza di ingresso dell’antenna alla sorgente del segnale. Questo può essere utile, ad esempio, quando l’antenna è collegata a un amplificatore o a un ricevitore con un’impedenza diversa da quella dell’antenna. In questo caso, l’antenna viene carica in modo da presentare un’impedenza di ingresso compatibile con quella della sorgente del segnale.
Infine, le antenne caricate possono essere utilizzate per focalizzare la radiazione in determinate direzioni. Ciò può essere ottenuto utilizzando carichi di induttanza o di capacità in modo selettivo, in modo da modificare la distribuzione della corrente lungo l’antenna e quindi la direzione di emissione del segnale.
In sintesi, le antenne caricate sono un’importante tecnologia che consente di adattare le proprietà elettriche delle antenne alle specifiche esigenze di progetto, per ottenere prestazioni ottimali in diverse applicazioni.
Dipolo ripiegato (folded dipole) e antenne a banda larga⌗
Un’altra variante del dipolo \( \lambda/2\) é costituita dal dipolo ripiegato (folded dipole). Quest’antenna realizzata congiungendo gli estremi di un dipolo \( \lambda/2\) con un conduttore parallelo a esso per simulare un dipolo \( \lambda/2\) avente un diametro del conduttore piú grande.
Poiché la banda di un dipolo aumenta con l’aumentare del diametro del conduttore, il dipolo ripiegato é un’antenna a banda larga utilizzata come elemento base delle antenne riceventi TV.
Il guadagno rimane lo stesso del dipolo \( \lambda/2\), la resistenza di radiazione quadruplica arricando a circa \(R_r = 300 Ω\). Questa antenna puó essere usata da sola oppure puó costituire l’elemento radiante di antenne piú complesse, come le antenne riceventi TV di tipo Yagi.
Antenne direttive⌗
Un’antenna che concentra la maggior parte della potenza irradiata lungo una direttrice ben precisa, viene definita direttiva unidrezionale, o piú semplicemente direttiva.
Le antenne direttive hanno le seguenti caratteristiche salienti:
- Guadagno piú alto;
- Non irradiano nelle aree che non interessa servire;
- L’antenna é adatta per collegamenti di tipo punto-punto;
Un parametro importante per le antenne direttive é l’FBR (Front-to-Back Ratio), che ne definisce il grado di unidirezionalitá. Piú alto é l’FBR e maggiore sará l’unidirezionalitá dell’antenna.
Diagramma di radiazione di un’antenna direttiva undirezionale Yagi:
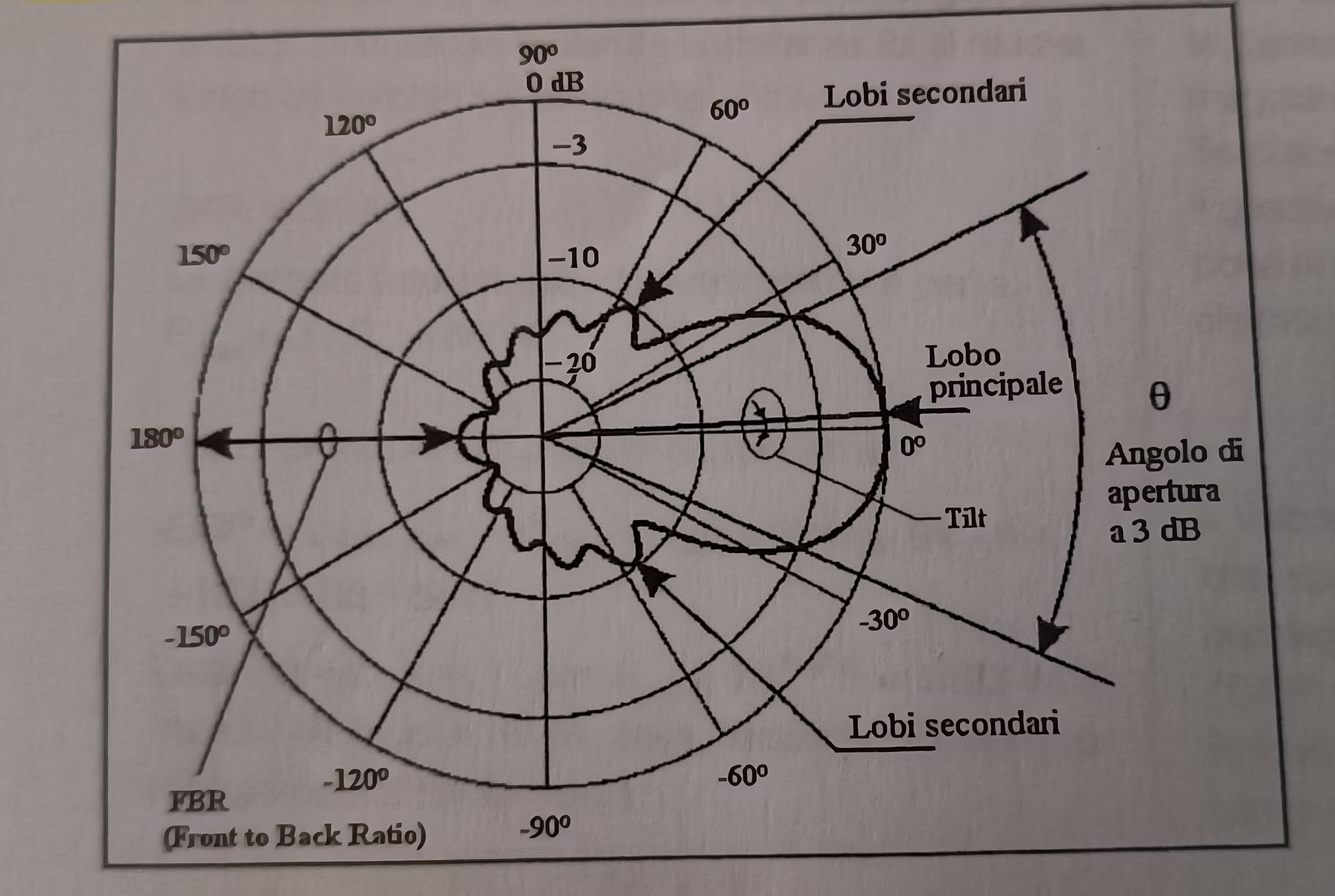
Angolo di apertura del fascio (beamwidth) o angolo di radiazione⌗
Viene definito angolo di apertura a 3 dB (beamwidth), o angolo di radiazione di un’antenna (\( \theta\) ), l’angolo indiviato dai due punto sul diagramma di radiazione in cui il grafico diminuisce di 3 dB rispetto al valore che si ha nella direzione di massimo irraggiamento.
Nelle due direzioni individuate dall’angolo \( \theta\) la densitá di potenza, \(S\), si dimezza, rispetto al valore nella direzione di massimo irraggiamento, e di conseguenza il campo elettrico, \(E\), diviene pari a \(E = E_{max \space IRR} / \sqrt{2}\).
Front-to-Back Ratio (rapporto avanti/dietro)⌗
Il Front-to-Back Ratio (FBR), o rapporto avanti/dietro, esprime il grado di unidrezionalitá di un’antenna direttiva.
L’FBR é espresso in decibel ed é pari alla differenza tra il guadagno (normalizzato) nella direzione di massima irradiazione (\( 0\degree\)) e il guadagno (normalizzato) che si ha nella direzione opposta (a \(180\degree\)gradi):
$$ \Large\textsf{}FBR = G (0\degree) - G (180\degree) $$
Antenna Yagi⌗
Un’antenna direttiva puó essere realizzata affiancando a un dipolo \( \lambda/2\) degli elementi passivi. Un elemento passivo é un conduttore, avente lunghezza appropriata, che viene posta nelle immediate vicinanze dell’elemento radiante. L’elemento passivo intercetta una parte dell’energia irradiata e a sua volta la reirradia.
L’antenna Yagi é composta da:
- Un elemento attivo costituito da un dipolo \( \lambda/2\)
- Un elemento passivo detto riflettore, avenete lunghezza maggiore di \( \lambda/2\) che riflette le onde elettromagnetiche nella direzione desiderata;
- Uno o piú elementi passivi, detti direttori, che hanno lunghezza minore di \( \lambda/2\) i quali concentrano la potenza irradiata nella direzione desiderata.
Facendo un’analogia ottica, il riflettore si comporta come uno specchio, mentre i direttori si comportano come delle lenti convergenti.
L’antenna Yagi é molto utilizzata come antenna ricevenete TV. Il riflettore tubolare puó essere sostituito da un riflettore formato da un diedro di materiale condutttore, sulla cui bisettrice viene posto il dipolo attivo. Si realizza cosí l’antenna a diedro o corner riflector.
Antenna collineari e a cortina⌗
Un modo per aumentare la direttivitiá e il guadagno di un’antenna é quello di utilizzare sistemi radianti costituiti da un certo numero ($N$) di dipoli \( \lambda/2\) allineati e alimentati. Se i dipoli sono disposti sullo stesso asse si ottiene un’antenna collineare o allineamento (array) collineare, mentre se i dipoli sono disposti a matrice su un piano si ottiene una cortina di dipoli.
In tal modo il guadagno rispetto al dipolo \( \lambda/2\), espresso in dBd, diventa pari a \(G = 10\log_{10}N d Bd\).
Puntamento delle antenne direttive⌗
Nel caso di collegamenti che impiegano antenne direttive, é importante conoscere il diagramma di radiazione per poter puntare correttamente l’antenna, cioé per posizionarla nella direzione in cui l’antenna capta meglio. Un errato puntamento dell’antenna causa una diminuzione del segnale fornito in uscita dall’antenna stessa, che puó anche annullarsi.
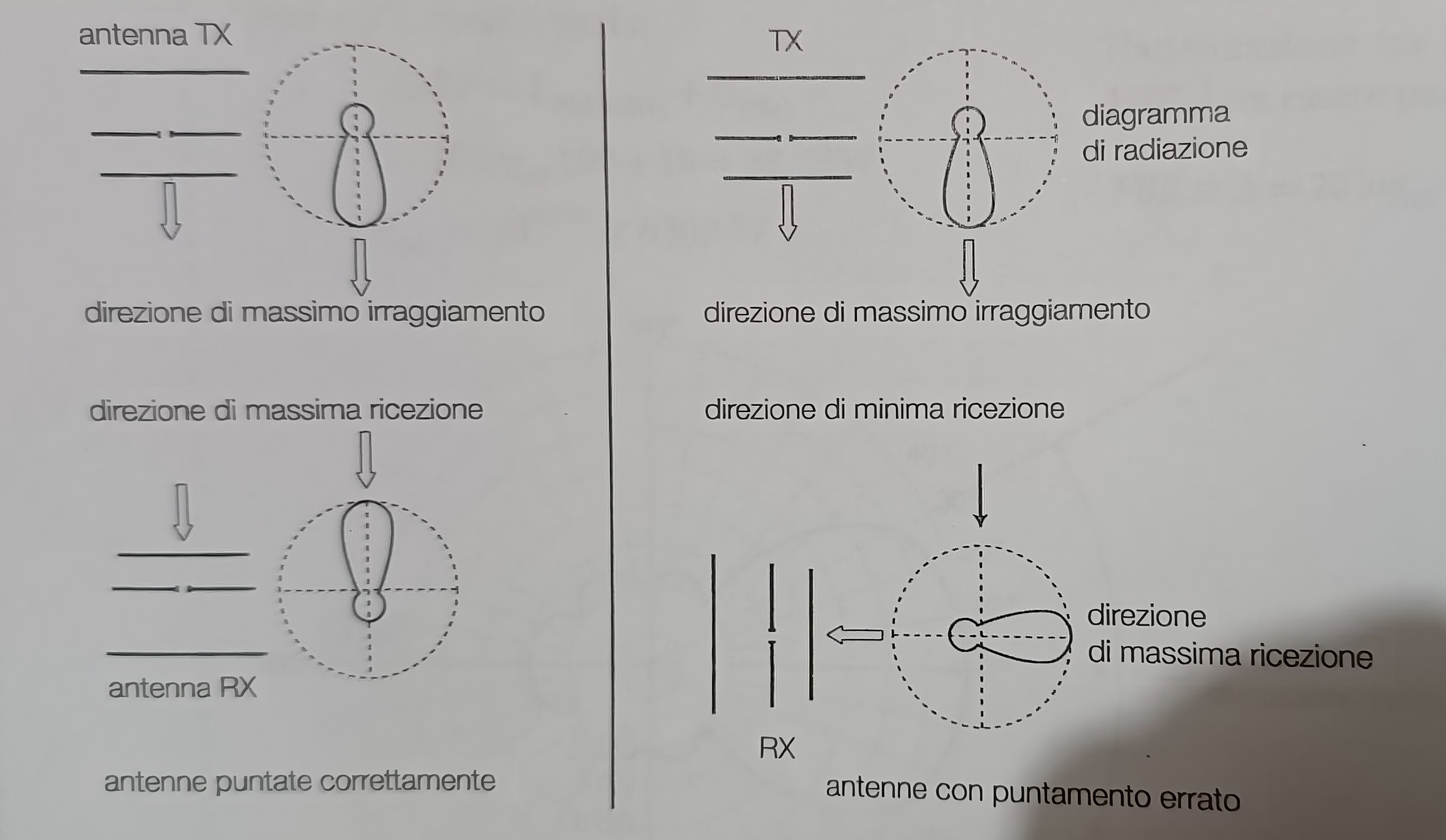
Antenne a superficie⌗
Quando si opera nel campo delle microonde (UHF, SHF, EHF) le onde radio possono essere considerate come dei raggi che é possibile riflettere e focalizzare tramite superfici di forma e materiale opprtuni.
Antenna parabolica⌗
Nel campo dell’illuminazione per ottenere uno stretto fascio luminoso é possibile utilizzare riflettori parabolici, ponendo una sorgente luminosa nel punto focale di una superficie riflettente a forma di paraboloide.
Se l’irradiazione di una sorgente, posta nel punto focale, viene riflessa da una superficie costituita da un paraboloide, la potenza irradiata viene concentrata in un fascio molto stretto lungo la direzione di propagazione, ottenendo cosí un elevato guadagno.
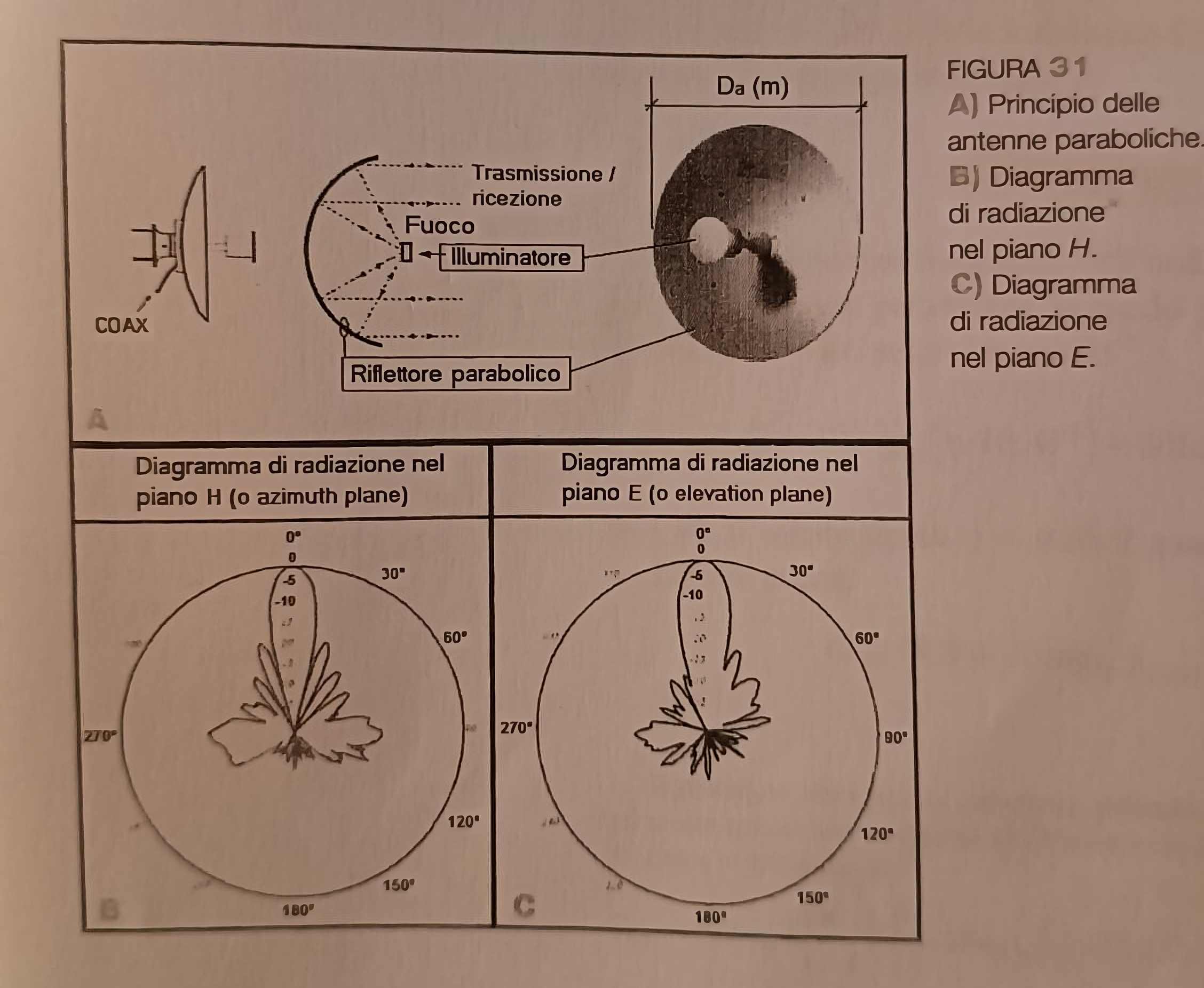
I diagrammi di radiazione nei piani \(H\) ed \(E\) mostrano un lobo principale molto pronunciato, con un angolo di apertura molto piccolo, che denota un elevato guadagno.
Per il principio di reciprocitá l’antenna conserva le sue proprietá anche quando viene usata come antenna ricevente. Il guadagno delle antenne paraboliche arriva a valori molto alti, anche 60 dB per antenne di grandi dimensioni.
L’illuminazione della superficie parabolica, cioé l’irradiazione delle onde elettromagnetiche verso la superficie riflettente, puó essere realizzata in vari modi:
- Un’antenna vera e propria posta nel fuoco della parabola;
- Una guida d’onda tronca o terminata a tromba posta nel fuoco della parabola;
L’illuminazione non é uniforme, ma decresce verso i bordi, l’illuminatore tende a illuminare meglio il centro. Per questo motivo si definisce l’efficienza, \( \eta\), di un’antenna parabolica come il rapporto tra l’area equivalente ( \(A_{eq}\) ), o area efficace e l’area geometrica ( \(A_g\) ) dell’antenna in esame: \( \eta = A_{eq} / A_g\). Normalmente si ha \(0,5 < \eta < 0,8\); in mancanza di dati certi si puó assumere il valore tipico \( \eta = 0,65\).
Il guadagno di una antenna parabolica dipende dalla sua efficienza, dal suo diametro ( \(D_a\) ) e dalla lughezza d’onda del segnale captato o irradiato secondo la seguente relazione:
$$ \Large\textsf{}G = 10 \log_{10} \eta \begin{pmatrix} \dfrac{\pi * D_a}{\lambda} \end{pmatrix}^2 ; [dB] $$
L’angolo di apertura a 3 dB (beamwidth) di un’antenna parabolica si puó calcolare come:
$$ \Large\textsf{}\theta\degree \approx 70 \dfrac{\lambda_{[m]}}{D_{a[m]}} $$
Parabola offset⌗
Le parabole che hanno l’illuminatore nel fuoco vengono denominate prime focus. Per limitare le interferenze sono state realizzate parabole denominate offset le quali sono costituite da una sezione di un paraboloide che punta verso un illuminatore posto nel fuoco, il quale però non è al centro dell’antenna bensì in posizione sottostante.
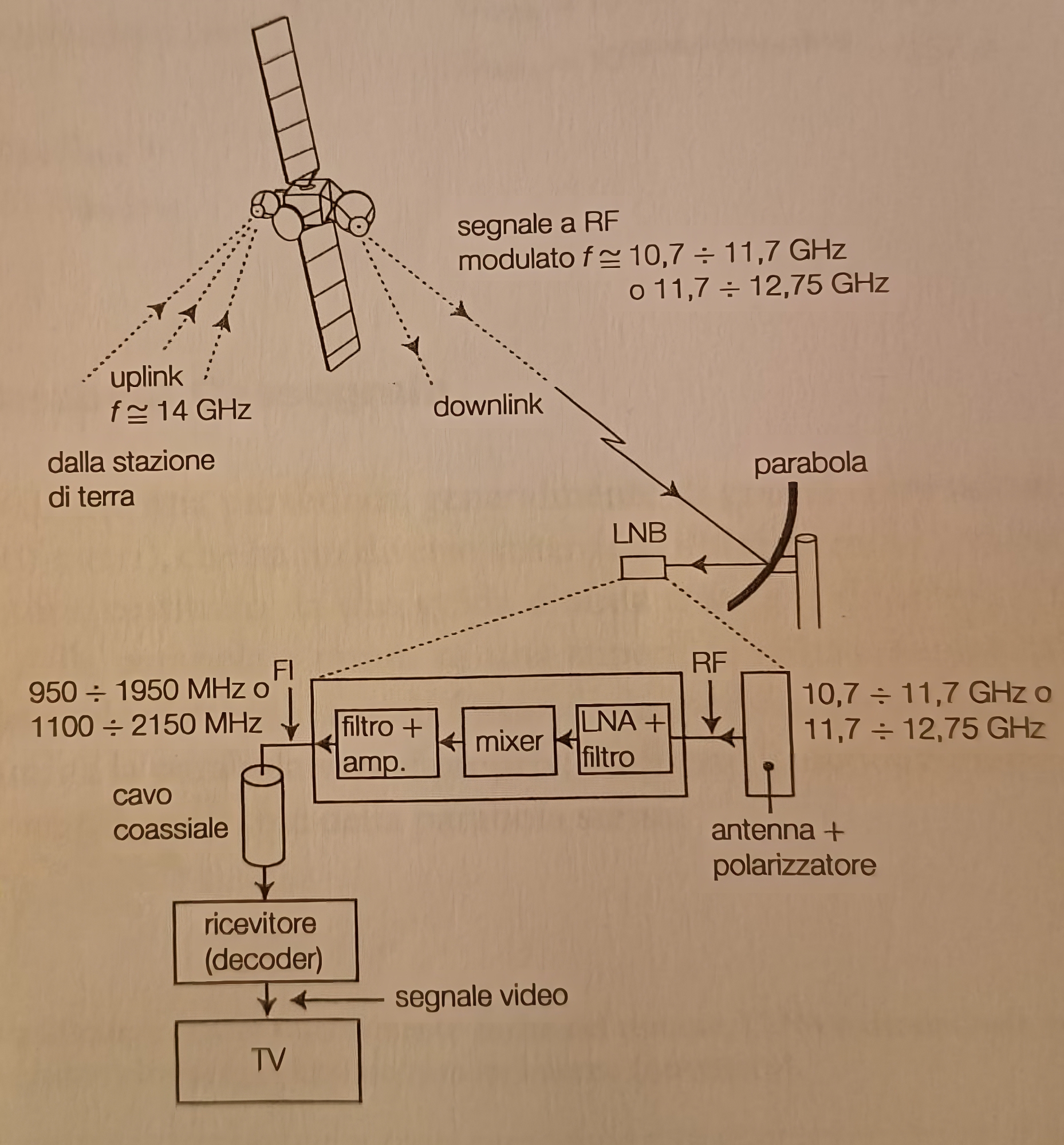
Antenne paraboliche per la ricezione TV da satellite⌗
L’antenna parabolica costituisce un’antenna direttiva ad alto guadagno utilizzata anche per la ricezione di segnali TV da satellite (sistema DVB-S, Digital Video Broadcasting-Satellite).
In questo caso sia perché l’intensità del segnale ricevuto è estremamente debole, sia perché la frequenza del segnale ricevuto è molto elevata, viene montato direttamente sulla parabola un dispositivo denominato LNB (Low Noise Black converter), collegato all’antenna ricevente vera e propria e a un polarizzatore, per discriminare il segnale in base alla sua polarizzazione.
L’LNB è composto fondamentalmente da tre parti:
- LNA (Low Noise Amplifer): è un amplificatore che eleva il livello del segnale RF ricevuto;
- Mixer o down converter: ha il compito di abbassare la frequenza del segnale captato portandola dalla radio frequenza a una frequenza detta frequenza intermedia (FI);
- Filtro passa banda e amplificatore a FI: per eliminare le frequenze indesiderate e amplificare il segnale a FI prima di inviarlo sul cavo coassiale;
Parabola Cassegrain⌗
È un tipo di antenna parabolica, che ha un diverso sistema di illuminazione, l’illuminatore, costituito da una guida d’onda tronca (feed horn), è posto al centro della parabola e punta su una superficie riflettente secondaria, denominata subriflettore, avente la forma di un iperboloide di rotazione, in questo modo si ottiene un’illuminazione più uniforme.
Sistemi di antenna MIMO(Multiple In Multiple Out)⌗
In alta frequenza, i sistemi d’antenna possono impiegare una o piú antenne e possono essere suddivisi nei seguenti sistemi:
- SISO (Serial In Serial Out): sono i sistemi che utilizzano un’antenna lato trasmissione e un’antenna lato ricezione; sono sistemi adatti a operare quando l’ambiente é assimilabile allo spazio libero.
- SIMO (Serial In Multiple Out): sono i sistemi che operano lato ricezione con due antenne riceventi, per implementare la tecnica della diversitá di spazio; sono adatti a operare quando il ricevitore é posto in un ambiente in cui vi sono oggetti che causano riflessioni.
- MISO (Multiple In Serial Out): sono un’alternativa ai sistemi SIMO, in cui si utilizzano due antenne trasmittenti e un’antenna ricevente.
- MIMO (Multiple In Multiple Out): sono i sistemi piú moderni che utilizzano contemporaneamente due o piú antenne in trasmissione e due o piú antenne in ricezione. Sono sistemi che trasmettono e ripartiscono il flusso di bit in ingresso su piú segnali modulati inviati in parallelo alle antenne trasmittenti; i segnali vengono captati dalle antenne riceventi e con sofisticate tecniche di elaborazione digitale dei segnali (DSP) sono demodulati e viene riassemblato il flusso id bit originario; i sistemi MIMO consentono di aumentare la capacitá trasmissiva di un sistema all’aumentaredel minimo tra (m, n), dove m é il numero di antenne usate in trasmissione e n é il numero di antenne usate in ricezione; possono operare in maniera piú efficace in ambienti in cui vi sono molte riflessioni in quanto sono in grado di compensare le differenze di fase fra i vari percorsi e quindi di sfruttare positivamente i segnali riflessi. I sistemi MIMO sono impiegati nei sistemi di comunicazione radio piú moderni; apparati WiFi (802.11n), sistemi di accesso wireless a banda larga (WiMAX), sistemi per la comunicazione in mobilitá di ultima generazione (LTE, Long Term Evolution).
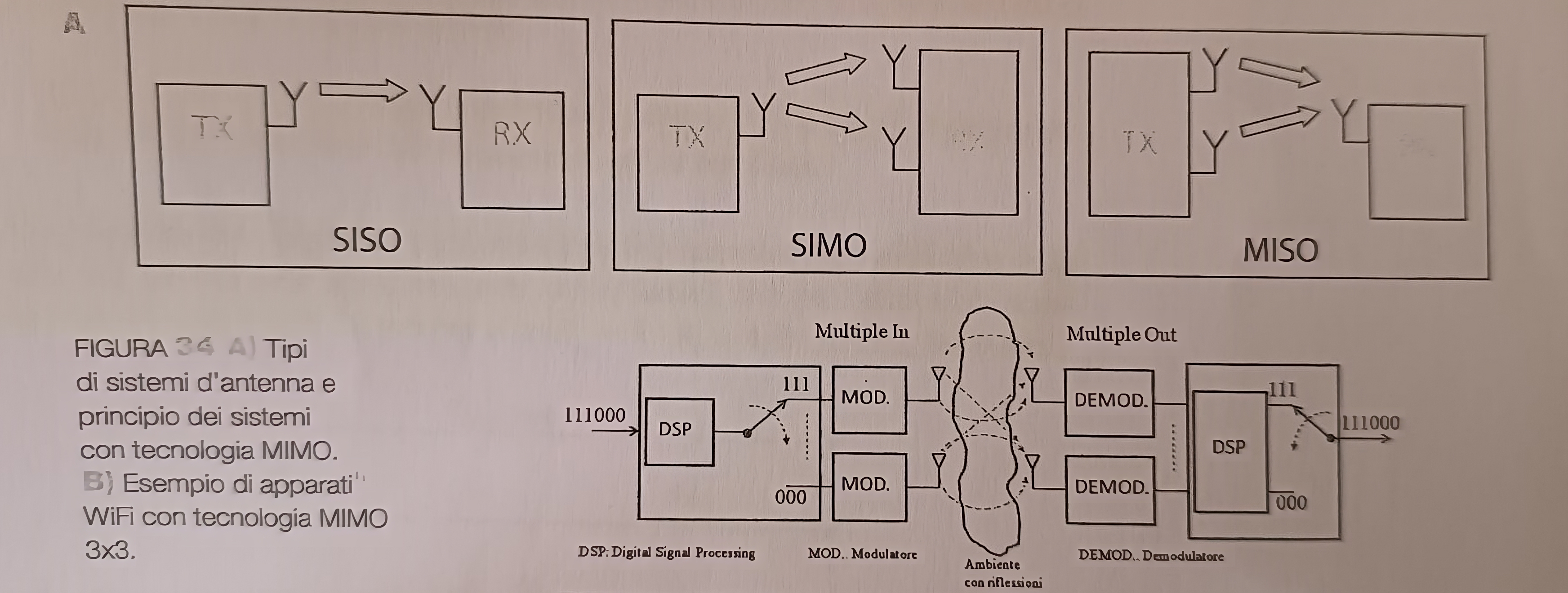
Installazione dei sistemi di antenna⌗
Quando si opera a frequena elevate (bande VHF/UHF/SHF) le onde elettromagnetiche si propagano per onda diretta, propagazione detta anche in visibilitá ottica (Line Of Sight - LoS).
Questo tipo di propagazione richiede che le antenne tramittenti e riceventi siano (quasi) visibili l’una all’altra, in quanto le onde elettromagnetiche viaggiano direttamente dall’antenna trasmittente all’antenna ricevente.
Nello spazio libero i percorsi seguiti sarebbero rettilinei, mentre nell’atmosfera essi risentono delle disomogeneitá del mezzo.
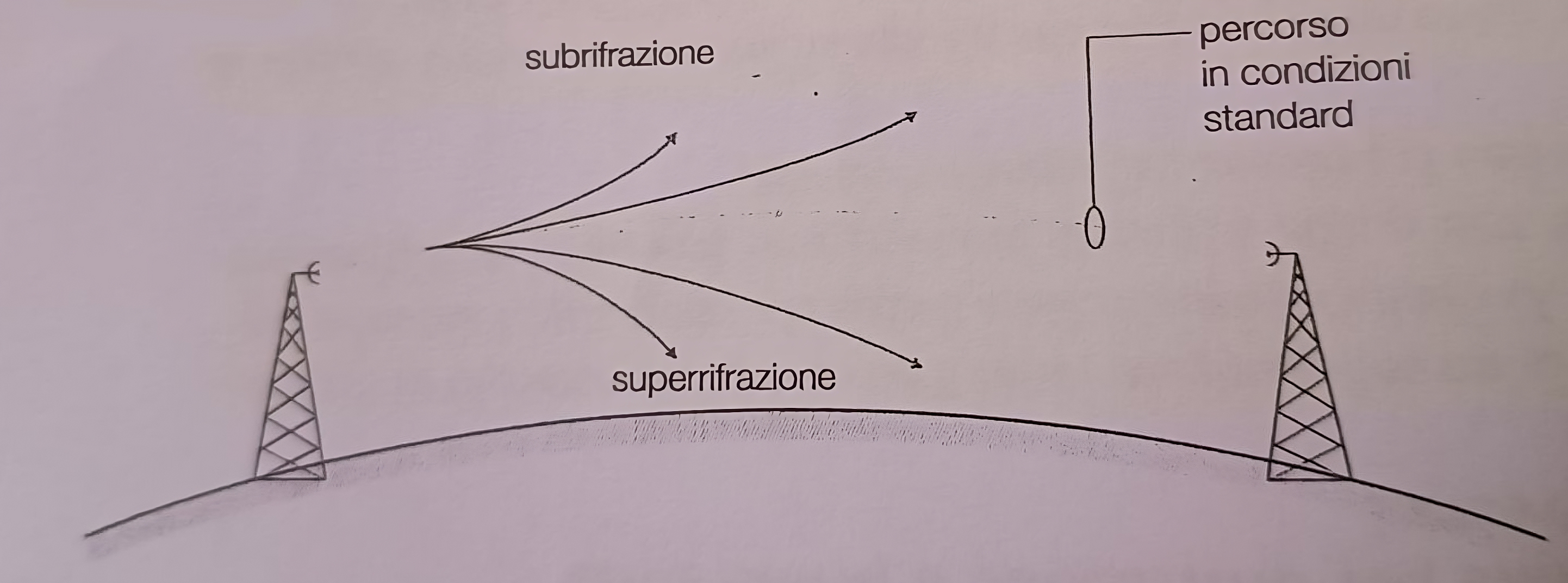
In condizioni normali (atmosfera standard) le disomogeneitá causano delle rifrazioni facendo sí che il percorso seguito da un’onda elettromagnetica sia all’incirca un arco di cerchio.
In situazioni anomale si possono avere rifrazioni diverse, fenomi di riflessione, diffrazioni e assorbimento, che causano ulteriori perdite. Tali fenomeni avvegono nella troposfera in quanto la stratosfera e la ionosfera a queste frequenze si possono considerare sostanzialmente simili allo spazio libero.
I calcoli relativi all’installazione e al posizionamento delle antenne sono semplificati se si considerano i percorsi come rettilinei. a tale scopo si tiene conto del fatto che in realtá i percorsi sono archi di cerchio, introducendo cosí il concetto di terra equivalente.
La terra equivalente é una superficie terrestre fittizzia in cui si possono considerare i percorsi delle onde elettromagnetiche come rettilinei.
Il raggio della terra equivalente si ottiene moltiplicando il raggio effettivo della terra per un fattore $k$ (effective earth radius factor), che per l’atmosfera standard vale \(k = 4/3 \approx 1,33\), per cui si ha \(R_{eq} = k * R_0 = 4/3 * 6367 \approx 8490\) km.
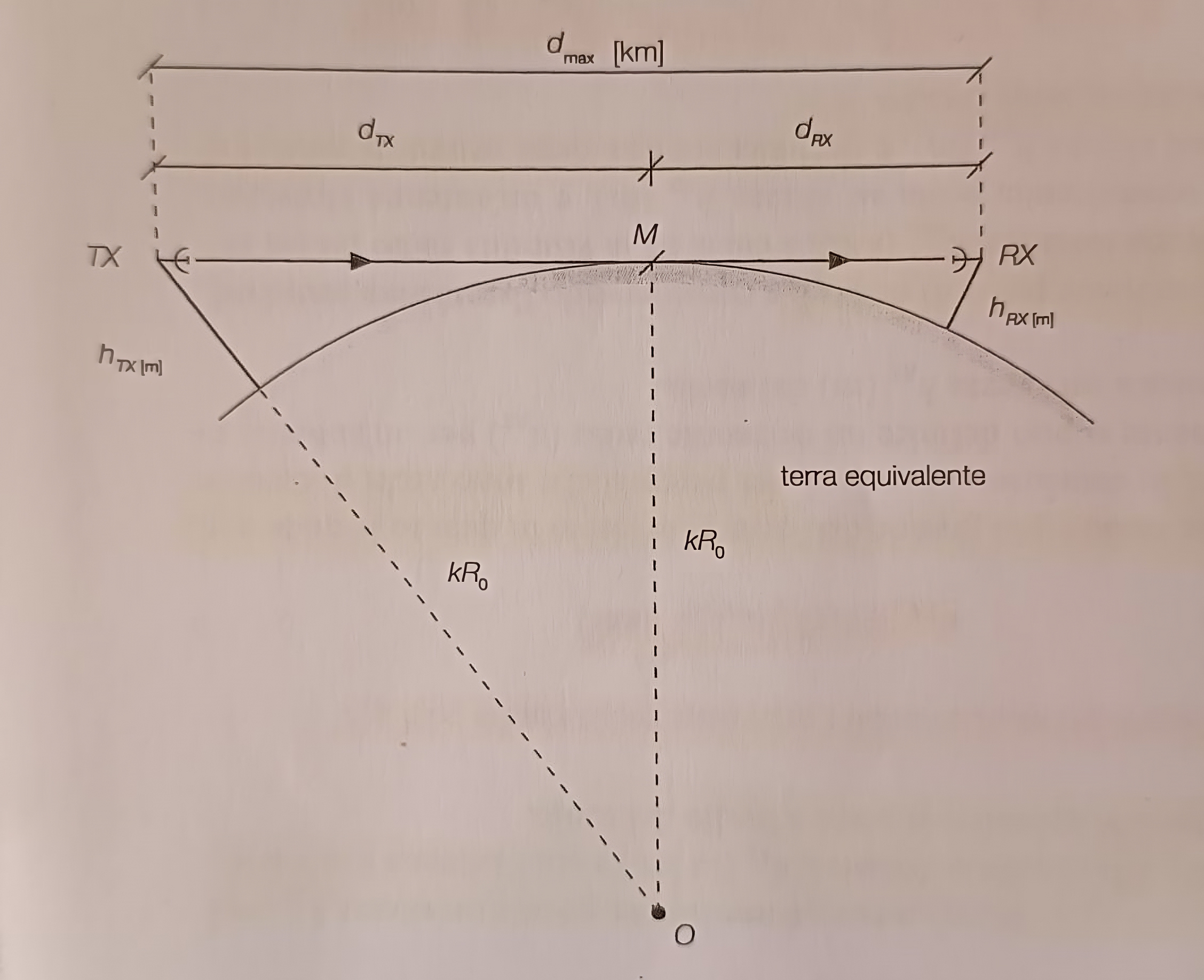
Orizzonte radio e massima distanza fra due antenne⌗
L’orizzonte radio di un’antenna trasmittente, posta a un’altezza \(h_{TX}\) (m) dal suolo, é la massima distanza, \(d_{TX}\) (in km) a cui l’altezza é in visibilitá radio con un’antenna posta a livello del suolo.
In un ambiente privo di ostacoli l’orizzonte radio risulta pari a:
$$ \Large\textsf{}d_{TX} \approx 4,12 \sqrt{h_{TX [m]}} ; [km] $$
L’orizzonte radio é piú grande dell’orizzonte visivo in quanto le onde elettromagnetiche compiono dei percorsi che sono archi di cerchio.
In un ambiente privo di ostacoli la massima distanza \(d_{max}\) é pari alla somma degli orizzonti radio e si puó calcolare come:
$$ \Large\textsf{}d_{max} = d_{TX} + d_{RX} \approx 4,12 (\sqrt{h_{TX_[m]}} + \sqrt{h_{RX_[m]}}) ; [km] $$
Quando le condizioni dell’atmosfera non sono quelle standard varia la curvatura della traiettoria del raggio. Si definiscono cosi le seguenti due condizioni:
- subrifrazione, quando \(k < 4/3\) e la curvatura é inferiore rispetto alla condizione standard; l’onda elettromagnetica (raggio) devia verso l’alto rispetto alla traiettoria standard;
- superrifrazione, quando \(k > 4/3 \); la curvatura é maggiore di quella standard; l’onda elettromagnetica (raggio) devia verso il basso rispetto alla traiettoria standard.
Queste situazioni possono comportare una diminuzione anche forte della potenza di segnale che giunge all’antenna ricevente e si configurano come una forma di fading.
Perdite per diffrazione e prima zona di Fresnel⌗
Quando in un collegamento radio il terreno (o un ostacolo di dimensione » \( \lambda\) ) risulta vicino alla linea fittizzia che congiunge l’antenna trasmittente con quella ricevente intervengono fenomeni di diffrazione che riducono la potenza del segnale ricevuto.
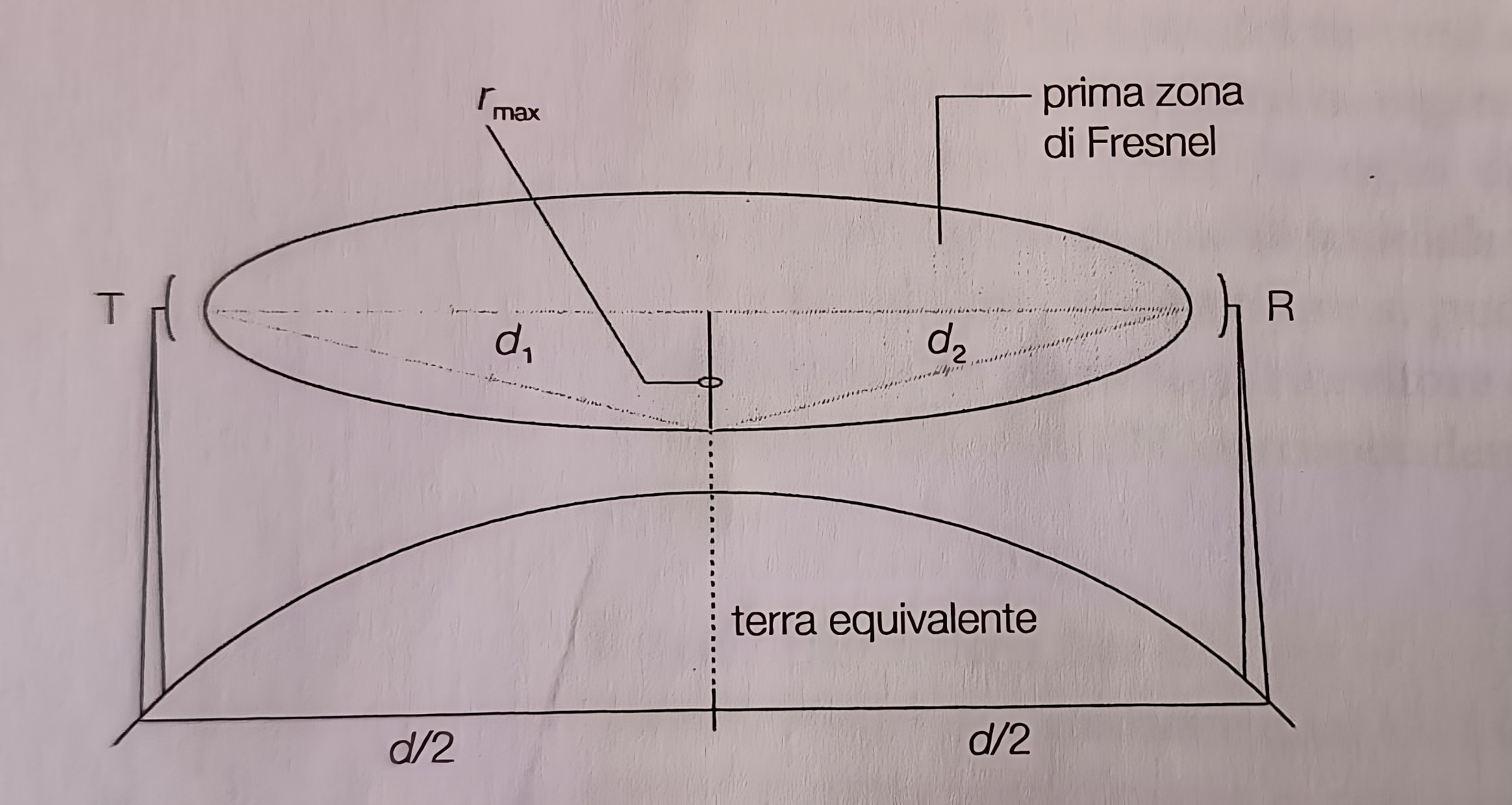
La maggior parte della potenza giunge all’antenna ricevente viaggia in una zona dello spazio denominata prima zona di Fresnel, individuata da un eliissoide di ratoazione detto ellisoide di Fresnel.
Il raggio massimo dell’ellissoide di Fresnel si ha quando \(d_1 = d_2 = d/2\), il raggio massimo dell’ellissoide di Fresnel risulta pari a:
$$ \Large\textsf{}r_{max} = 8,66 \sqrt{\dfrac{d_{km}}{f_{GHz}}} ; [m] $$
Le perdite per diffrazione sono trascurabili solo se la prima zona di Fresnel risulta libera da ostacoli. Quindi l’altezza delle torri o dei tralicci viene calcolata imponendo che eventuali ostacoli risultino posti a distanze maggiori di \(r_{max}\).
Dimensionamento di un collegamento radio⌗
È necessario fare il bilancio di potenza di un collegamento, o link (power) budget, per calcolare qual è il livello di potenza che si fornisce in ingresso al primo amplificatore in ricezione.
Bilancio di potenza (link budget) di un collegamento radio⌗
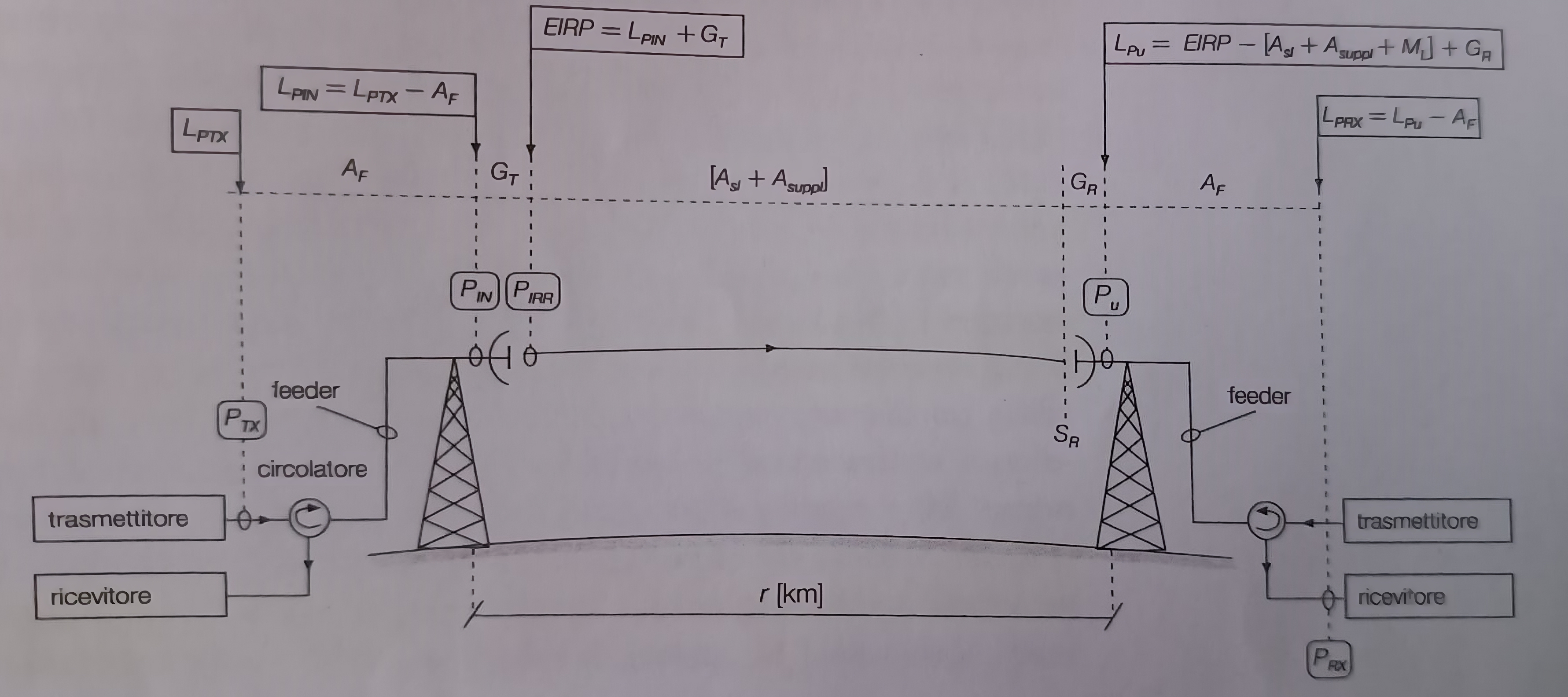
Il bilancio di potenza di un collegamento radio è una relazione matematica che lega il livello di potenza con cui opera il trasmettitore al livello di potenza che si ha in ingresso al ricevitore, sommando tutti i guadagni e sottraendo tutte le attenuazioni che sono presenti fra uscita del trasmettitore e ingresso del ricevitore:
$$ \Large\textsf{}L_{PRX} = L_{PTX[dBm \ (o \ dBW)]} + \sum Guadagni_{[dB]} - \sum Attenuazioni_{[dB]} ; dBm\ (o \ DBW) $$
Spesso si preferisce spezzare il bilancio di potenza in due parti:
- Calcolo dell’EIRP del sistema tramittente, sottraendo al livello di potenza del trasmettitore ( \(L_{PTX}\) ) l’attenuazione del feeder (cavo) \(A_F\) in dB, e sommando il guadagno dell’antenna trasmittente ( \(G_T\) in dBi);
- Si calcola il livello in ricezione sottraendo all’EIRP l’attenuazione del collegamento radio, tenendo conto dell’attenuazione dello spazio libero ( \(A_{sl}\) ) dell’eventuale attenuazione supplementare (\( A_{suppl}\) ), sommando il guadagno dell’antenna ricevente e sottranendo l’attenuazione dell’eventuale feeder (cavo), \(A_F\).
Calcolo del livello in ricezione⌗
Per calcolare il livello in ricezione si procede nel seguente modo:
-
Determiniamo l’EIRP del sistema trasmittente.
-
Calcoliamo il livello di potenza del trasmettitore esprimendo la potenza in \( mW \) e applicando la relazione:
$$ \Large\textsf{}L_{PTX} = 10\log_{10} \ P_{TX[mW]} [dBm] $$
-
Calcoliamo l’attenuazione del cavo coassiale (feeder), l’attenuazione per unità di lunghezza (\( \alpha \)) e la sua lunghezza ( \(l\) ) come:
$$ \Large\textsf{}A_F = \alpha * l [dB] $$
-
Noto il tipo di antenna e le sue caratteristiche si determina il guadagno ( \(G_T\), in \(dBi\), o semplicemente in $dB$ per le antenne paraboliche).
-
Si calcola l’EIRP:
$$ \Large\textsf{}EIRP = L_{PTX [dBm]} - A_{F[dB]} + G_{T[dB]} [dBm] $$
-
-
Determiniamo l’attenuazione del collegamento radio.
-
Calcoliamo l’attenuazione dello spazio libero ( \(A_{sl}\) ) e la distanza fra le antenne \((r)\) in km:
$$ \Large\textsf{}A_{sl} = 32,5 + 20\log_{10} f_{MHz} + 20\log_{10} ; r_{km} [dB] $$
Se si opera a frequenze elevate, si dovrebbe verificare che l’altezza sia sufficiente per fornire la visibilitá radio fra le antenne.
-
Stimiamo l’attenuazione supplementare ( \(A_{suppl}\) ); indicativamente in ambiente aperto e in situazioni meteo favorevoli l’attenuazione supplementare é trascurabile per frequenze inferiori ai \(10 GHz\), \(0,02 dB/km\) a circa \(0,2 dB/km\) fino a \(40 GHz\).
-
Si introduce un margine del collegamento, o margine di link (\(M_L\)) per tener conto dell’aumento di attenuazione che si potrebbe avere in determinate condizioni atmosferiche. \(M_L\) é legato alla frequenza di trasmissione e alla disponibilitá che si desidera ottenere per il collegamento.
Nei collegamenti terrestri si puó aggiungere nel margine di link anche un margine contro i fading (margine di fading, \(M_F\)).
-
-
Determiniamo il livello di potenza in ingresso al ricevitore.
-
Noto il tipo di antenna ricevente e le sue caratteristiche se ne determinina il guadagno (\(G_g\), in dBi, o dB per le antenne paraboliche).
-
Si calcola l’attenuazione del feeder in ricezione.
-
Si calcola il livello di potenza in ingresso al ricevitore:
$$ \Large\textsf{}L_{PRX} = EIRP - [A_{SL} + A_{suppl} + M_L] + G_R - A_{FRX} dBm $$
-
-
Si verifica che il livello in ricezione sia almeno pari alla sensibilitá del ricevitore affinché il sistema fornisca in uscita un segnale con livello e qualitá accettabile:
$$ \Large\textsf{}L_{PRX_[dBm] } \geq S_{RX_[dBm]} $$
Utilizzando la stessa metedologia é possibile, variando i dati, determinare un’incognita diversa:
- Distanza massima del collegamento
- Guadagno che deve avere l’antenna ricevente
- Margine di link che si ha
Fading delle Antenne⌗
Il fenomeno del fading delle antenne si riferisce alla perdita di intensità del segnale radio quando viene trasmesso da un’antenna e ricevuto da un’altra. Questo può accadere a causa di diverse ragioni, tra cui l’effetto della riflessione, la diffrazione e l’assorbimento delle onde radio.
In particolare, il fading può essere causato dalla riflessione delle onde radio su superfici come edifici, alberi o montagne, che possono creare zone di attenuazione o interferenza nel segnale radio. Inoltre, il fading può essere causato dalla diffrazione, cioè dalla deviazione del segnale radio quando incontra ostacoli come angoli, spigoli o superfici curve.
Il fading può anche essere causato dall’assorbimento delle onde radio da parte di materiali come acqua, pioggia, neve o aria umida. In questo caso, la quantità di energia del segnale radio diminuisce man mano che attraversa questi materiali, causando un attenuamento del segnale.
Il fading può essere ridotto utilizzando tecniche come l’uso di antenne direzionali, la diversità di antenna e la modulazione adattiva, che possono aiutare a migliorare la qualità del segnale radio e ridurre la perdita di intensità.